Предикати. Формальні теорії

Предикатом Р(х₁, ...х_n) називають логічну функцію n змінних, не обов’язково логічних. Наприклад, предикат 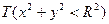перевіряє розміщення точки з координатами (х, у) в середині кругу з радіусом R з центром на початку координат.

У числення предикатів входять квантори існування 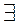(читається „існує”) та 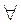(читається „для всіх”). Змінна, за якою береться квантор на множині його дії, називається зв’язаною. Ім’я цієї змінної можна довільно змінювати за умови, що вона не буде співпадати з іменами інших змінних у формулі. Приклади зображення знань з використанням предикатів із кванторами:

а) 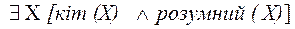: - деякий кіт має розумові здібності;

б) 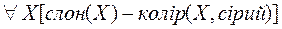– усі слони сірі (рідко зустрічаються цінні білі слони).

Формулу, що не містить х, можна виносити за область дії квантора, що зв’язує х.

При інтерпретації предикатів можливі три основних ситуації:

1) формула виконується, тобто існує набір постійних, який робить предикат здійснюваним: ;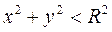

2) формула виконується для будь-яких наборів (є загальнозначущою): ;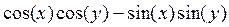

3) формула не виконувана (суперечлива): .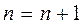

Приклади загальнозначущих формул числення предикатів:

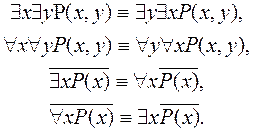
Синтаксичну структуру понять предметної області зазвичай описують деякою формальною теорією. Теорія доведень має допомагати отримувати формальними методами нові твердження про властивості об’єктів чи явищ предметної галузі, які є змістовною інтерпретацією формул, що виводяться. До алфавіту мови системи входять предметні константи, предметні змінні, предикатні змінні, логічні зв’язки та квантори, допоміжні символи (дужки, коми тощо). Множина слів мови складається з правильно побудованих формул (ППФ). Це, перш за все, аксіоми, що задаються при побудові теорії. Правила виведення дають змогу отримувати з аксіом ППФ-теореми. Множина аксіом називається незалежною, якщо жодну з них не можна вивести із сукупності тих, що залишилися. Часто для спрощення доведення теорем до системи аксіом включають також і залежні.

Безпосередня можливість виведення F з F₁, F₂, F₃,..., F_n записується у вигляді:

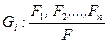
(над рискою розташовані істинні посилання, під рискою – висновок).

Факт виведення позначається F₁, F₂,...,F_n ├ F. Мітка G_i слугує для посилання на правило.

У формальних системах логічного типу до множини аксіом завжди входять логічні, використання яких поряд із специфічними для даної теорії правилами виведення дає можливість формалізувати процес доведення. Логічне числення називається несуперечливим, якщо в ньому не виводяться одночасно F та 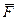. У суперечливих численнях виводиться будь-яка формула, що можна використати для доведення несперечливості числення: достатньо показати існування в ньому формули, що не виводиться.