Числення висловлювань

Числення висловлювань здійснює формальне виведення істинності складних висловлювань та еквівалентні перетворення висловлювань. За цих умов відбувається абстрагування від змістової основи висловлювання таким чином, що висловлювання „у городі бузина” та „в Києві дядько”, якщо обидва вони істинні чи обидва хибні, є формально еквівалентними. Двійкова алгебра утворюється константами 1 („істина”) та 0 („хибність”) та виконуваними над ними операціями. Їх істинність наведена у таблиці 1:

Найменування функції	Позначення функції	Значення функції за
х1=0
х 2=0
Заперечення Диз’юнкція Кон’юнкція Імплікація Еквівалентність	⌐x1; x1

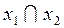
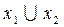
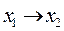
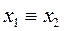
Важливу роль відіграють тотожно істинні формули-тавтології

Будь-яку логічну функцію можна виразити через значення вихідних змінних за допомогою операцій заперечення, диз’юнкції та кон’юнкції , наприклад, у диз’юнктивній нормальній формі. Для цього слід виписати диз’юнкцію тих добутків змінних, на яких функція є істинною, і в цих добутках замінити одиниці змінними, а нулі – запереченнями змінних. Наприклад, для імплікації:

.

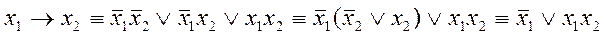Логічні функції реалізуються за допомогою комбінаційних схем.

Розглянемо питання щодо застосування багатозначних логік. За допомогою тризначної логіки описують, наприклад, стан контактів реле (норма, розрив кола, коротке замикання). Для базису {«хибність», „невизначеність”, „істина”} чи еквівалентного йому {-1, 0, 1} матиме місце таблиця істинності основних функцій:

Таблиця 2

Функції тризначної логіки

х1	-1
х2	-1			-1			-1
⌐x1 х1 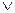х2 х1 х2	-1 -1	-1	-1	-1			-1 -1	-1	-1

Іншим, складнішим класом математичних об’єктів (відповідно – пристроїв) є скінченні автомати. Вважаючи вхідні та вихідні сигнали схеми з пам’яттю двійковими кодами букв певних абстрактних алфавітів Х та У, маємо змогу інтерпретувати роботу автомата як відображення вхідних слів у вихідні. Останнє залежить від стану автомата. Завжди можна спроектувати автомат, що реалізує будь-яку скінченну таблицю відображення, а далі мінімізувати його схему.