Нечіткі множини та нечітка логіка
Постановка задачі часто містить елементи невизначеності, яка необов’язково має імовірнісну природу. Зокрема, вона може бути лінгвістичною, випливати із властивостей мови опису задач. Такі характеристики, як „великий”, „малий”, „старий”, „міцний”, „швидкий”, не визначають кількісної міри, мають міцну контекстну залежність (молодий пенсіонер може бути старшим старого атлета, а карликовий гіпопотам – більшим за велику мишу). Людина може приймати рішення (можливо, не найкращі, але, у всякому разі, прийнятні) в умовах, які з різних точок зору містять невизначеність чи нечіткість. Вона оперує з нечіткими цілями та ідеями: використовує методи, які не є строго визначеними; приймають рішення у ситуаціях з неповною інформацією. Бажано надати такі здібності також і системам штучного інтелекту. Так, системи автоматичного управління, побудовані на основі нечіткої логіки, виявилися „уважнішими” до основного сигналу і не менш чутливими до шумів.
Нечітка (розмита) множина є сукупністю впорядкованих пар
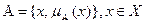 ,
,
де 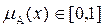 – функція належності елемента х до множини А. Вважається, що
– функція належності елемента х до множини А. Вважається, що
а) А=В, якщо 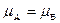 для всіх
для всіх 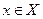 ;
;
б) 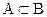 , якщо
, якщо 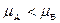 ;
;
в) 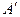 є доповненням до А, якщо
є доповненням до А, якщо 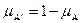 .
.
Остання умова передбачає нормування міри належності по всім елементам розглядуваної множини. У задачах діагностики вважається, що стан „підтверджено”, якщо показник довіри (значення ступеня належності) вищий верхнього порогу, та „відкинуто” – якщо він нижчий нижнього. Шлях виведення продовжується від підтвердженого стану, чи від стану з найбільшою вагою.
Зведення до позитивного ступеня α функції належності дає змогу перерозподіляти її значення між елементами множини. Якщо α>1, то різниця значень поглиблюється, коли ж α<1, то значення вирівнюються.
Міра належності х результатові операцій над множинами визначається таким чином:
1) для перетину 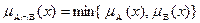 ,
,
2) для об’єднання 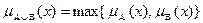 ,
,
3) для диз’юнктивної суми 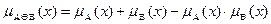
Нехай 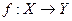 – чітке відображення,
– чітке відображення, 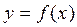 – образ х, а
– образ х, а 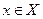 – прообраз у. Множина всіх прообразів елементу х позначається як
– прообраз у. Множина всіх прообразів елементу х позначається як 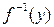 . Якщо А – нечітка множина в Х із заданою функцією належності
. Якщо А – нечітка множина в Х із заданою функцією належності 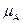 , то її образом при відображенні f називається розмита множина
, то її образом при відображенні f називається розмита множина 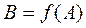 з функцією належності
з функцією належності
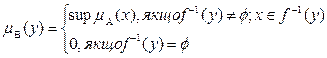
Якщо В – розмита множина в У із заданою функцією належності 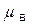 , то прообразом цієї множини при відображенні f називається розмита множина
, то прообразом цієї множини при відображенні f називається розмита множина 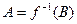 з функцієюналежності
з функцієюналежності 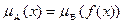 . Нехай В(х) – розмита множина в просторі У, а функція належності
. Нехай В(х) – розмита множина в просторі У, а функція належності 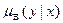 залежить від х, як від параметра. Тоді
залежить від х, як від параметра. Тоді 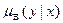 визначає нечітке відображення Х в У. Образом розмитої множини А в Х у цьому випадку є розмита множина В з функцією належності
визначає нечітке відображення Х в У. Образом розмитої множини А в Х у цьому випадку є розмита множина В з функцією належності
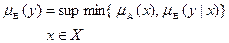 .
.
Розмитий розв’язок вибирається при нечіткій цілі G та нечітких обмеженнях С. Розв’язок визначається як Д-перетин G та С. Розмитий розв’язок можна розглядати як нечітко сформульовану інструкцію. Можна вибрати альтернативу, що має більший ступінь належності до Д. Можливі випадки, коли деякі цілі (обмеження) важливіші за інші. Розв’язок може бути визначений як розмита множина Д із функцією належності:
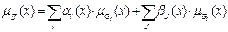 , де
, де
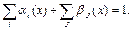
У загальному випадку цілі та обмеження зазначаються в різних підпросторах, коли заданим є відображення 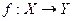 . У цьому випадку цілі {Gi} можна зобразити у вигляді розмитих множин
. У цьому випадку цілі {Gi} можна зобразити у вигляді розмитих множин 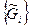 в Х, які є прообразами множин {Gi} відображення f , тобто
в Х, які є прообразами множин {Gi} відображення f , тобто 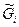 = f -1{Gi} та
= f -1{Gi} та 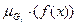 . Тоді функція належності розв’язку Д визначається рівністю
. Тоді функція належності розв’язку Д визначається рівністю
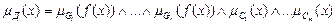 .
.
Дата добавления: 2015-04-01; просмотров: 1789;
