Продукції як алгоритмічна система. Ігри та рішення

Будь-яку формальну систему, що оперує символами, можна реалізувати продукційною системою Поста. Така система задається своїм алфавітом C={С₁,С₂,…,C_n} та системою базисних продукцій

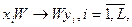
де х_і, у_і, W – слова в алфавіті С. Нехай слово Ψ починається півсловом х_і. Застосувати до Ψпродукцію означаєвикреслити з Ψ початковий відрізок х_і , потім до залишку дописати праворуч у_і. Наприклад, застосовуючи до слова ава продукцію авW – Wс, отримаємо слово ас.

Продукційна система на черговому кроці роботи в загальному випадку

а) вибирає продукцію з істинною умовою;

б) виконує вказану у ній дію;

в) змінює розв’язувальну умову деякої іншої продукції.

Продукції є певним чином впорядковані, після обробки кроку перевірка застосовуваності поновлюється починаючи з найбільш пріоритетної продукції. Цей цикл триває до виявлення тупику чи до застосування продукції, позначеної як завершальна. Продукційні системи можуть управлятися даними (передумови правил) та цілями (дії правил) та цілями (дії правил). У найбільш розвинених системах механізм вибору може мати ієрархію правил, мету правил чи складні системи управління, подібні до мереж Петрі. Продукцію часто використовують у комбінації з фреймами. Для фреймів-правил характерним є наявність:

1)кількох умов та дій для різних рівнів аналізу правила;

2)описових (невиконуваних) слотів, які можна використати як мета-правила для управління.

У традиційному програмуванні всі місця розгалуження вказуються явно, такий спосіб зручний, якщо розгалуження є скоріше винятком ніж нормою. У задачах ШІ, розв’язуваних на основі продукцій, програму краще розглядати як сукупність незалежних модулів, керованих зразками. З кожним кроком роботи така програма аналізує поточну ситуацію і за результатами аналізу визначає її обробника. Особливості цього підходу, з точки зору зображення знань такі:

1)Розділення постійних знань, що зберігаються у базі знань (БЗ), та тимчасових – у робочій пам’яті;

2) структурна незалежність модулів (полегшуються їх розроблення та модифікація);

3) відокремлення схеми управління від модулів.

Системи ШІ зазвичай використовуються для підтримки прийняття у людино-машинних системах. У багатьох випадках доводиться мати справу з проблемою прийняття рішень за умов невизначеності. Невизначеними можуть бути об’єктивні умови виконання операції, свідомі дії суперника (конкурента) чи інших осіб, від яких тією чи іншою мірою залежить успіх операції. Прийняті у таких випадках рішення виявляються не такими ефективними, як у цілком детермінованій ситуації, і зниження ефективності можна розглядати як збитки від неповноти інформації. Проте, кількісний аналіз ситуації допомагає прийняти найкраще за даних умов рішення. Математичні методи визначення оптимального рішення за умови невизначеності складають предмет теорії ігор та статистичних рішень.

На систему ШІ військового призначення, правоохоронних органів, конкурентної економіки може бути покладено завдання аналізувати конфліктні ситуації, в яких сторони, що стикаються, мають різні цілі. Будь-яке рішення у таких випадках повинно прийматися з врахуванням свідомої протидії розумного суперника. До конфліктних ситуацій призводять задачі розгляду динаміки бойових дій процесу перехоплення цілі, що ухиляється, вибору систем озброєння тощо. Спрощена та формалізована модель конфліктної ситуації називається „грою”. Вважається, що гра ведеться за правилами, які визначають можливі варіанти дій учасників, об’єм інформації однієї сторони про стан та дії іншої, порядок дій сторін та кількісний результат, що породжується даною сукупністю дій.

Розвиток гри у часі видається послідовністю ходів, які поділяються на особисті (за вибором учасників) та випадкові. Залежно від числа варіантів дій, ігри можуть бути скінченими та нескінченними. Стратегія гравця є правило, що визначає вибір варіанту дій g_i(t_j) на кожному кроці цього гравця. Якщо цей вибір задається розподілом імовірностей варіантів, стратегія називається змішаною. Гра закінчується визначенням її результату. Як правило, це певне число. В іграх із суворим суперництвом (з нульовою сумою) виграш одного гравця дорівнює програшу іншого. У цьому випадку гра описується платіжною матрицею L={L(S_i,t_j)} одного гравця, з розмірністю mxn. Один із гравців намагається максимізувати свій виграш, інший – мінімізувати програш. Очевидно, що 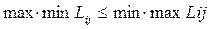. У випадку їх рівності матриця має сідловий елемент, одночасно мінімальний у стрічці і₀ та максимальний – у стовпці j₀ . Кожний гравець може бути покараний суперником за намагання ухилитися від стратегії з цієї пари (розв’язок гри у чистих стратегіях). За умови відсутності сідлового елементу матиме місце розв’язок у змішаних стратегіях (для ігор m x 2 та 2 x n – графічним методом, а у загальному випадку – методами лінійного програмування чи ітерації). Розмірність задачі може бути зменшеною виключенням стратегій, напевно невигідних сторонам. Якщо другим гравцем є об’єктивна дійсність, то кажуть про ігри з природою, чи стратегічні ігри.

В „іграх супроти природи” необов’язково розраховувати на найгірший варіант. У задачі теорії статистичних розв’язків можливі різні підходи до прогнозування дій природи. Критерій Вальда рекомендує вибір стратегії за мінімальним програшем, критерій Севіджа – за мінімумом максимального ризику внаслідок хибного рішення. Обидва вони є вкрай песимістичними. Критерій Гурвиця базується на притаманному ступені оптимізму 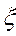, , 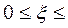з яким для кожної стратегії зважуються, відповідно, мінімальний і максимальний програші. Байєсівський підхід базується на мінімізації очікуваного (усередненого за розподілом імовірностей природи) програшу. Аналоги розрахованих підходів можна побудувати на основі нечіткого опису станів природи.