Динамічне програмування

Динамічним програмуванням (ДП) називають метод оптимізації, який базується на багатокрокових операціях: планування часової чи іншої послідовності дій. Припустимо, що з кожним кроком планованого процесу

1) його стан описується вектором Р;

2) вибраний розв’язок можна зобразити вектором Q;

3) новий стан на (і+1)-му кроці є відомою функцією попереднього стану та останнього прийнятого рішення:

4) з кожним кроком процесу пов’язаний дохід R_i (P_i, Q_i);

5) доходи, отримані на окремих етапах, підсумовуються.

За цих умов f_i,_n (сумарний дохід за n кроків, починаючи з і-го) залежить тільки від початкового стану Р_і та розв’язку Q_i поведінка на етапах, що залишилися, має бути оптимальною щодо нового стану 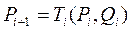– принцип оптимальності Р.Беллмана, тобто максимум згаданого доходу становитиме

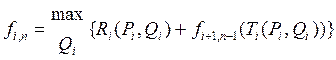
Очевидно, що .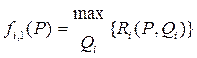

Задачі ДП у загальному випадку розв’язуються шляхом напрямленого перебору. Сутність цього методу така. Спочатку приймається, що стани {P_i}та розв’язки{Q_i} – скалярні величини. Далі проводиться дискретизація задачі, для спрощення припускають, що множина станів P={P₁,P₂,…,P_k} та множина розв’язків Q={q₁,q₂,…,q_L} є незалежними від номера періоду. Складається таблиця доходів {R_і} та нових станів {P_i+1} для всіх можливих комбінацій вихідних даних. Ці таблиці в окремих випадках можна замінити аналітичними залежностями. Далі задаються початковий стан Р₁ та якась -етапна поведінка {Q₁,Q₂,…,Q_n}. Тоді, користуючись таблицею {Т_i} знаходимо всю послідовність станів {P₁,P₂,…,P_n}, що проходить системою, а використовуючи {R_і}, визначають дохід на кожному кроці. Сума окремих доходів дає загальний дохід за певне число кроків. Оскільки можливо всього L^N різних типів поведінки, то оптимальну стратегію можна знайти повним перебором L^N варіантів, кожний з яких потребуватиме звернення до (2N-1) таблиць.

Принцип оптимальності дає змогу виконати напрямлений перебір, пов’язаний зі значно меншим обсягом обчислень. Цей перебір складається із зворотного і прямого ходів. Зворотний хід починається із знаходження максимумів

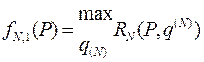
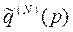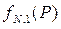доходів за останній (N-й) період для всіх можливих станів. Далі фіксується поведінка та доходи у таблицях та . Розглядаючи всі можливі стратегії для стану р перед двома останніми етапами, обчислюють суми

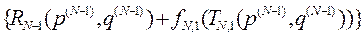, вибирають їх максимуми за кожного р, будують таблиці 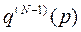та 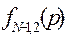і т.д., продовжуючи цей процес у напрямі до першого періоду, у кінці отримують 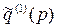та 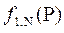. Стрічка 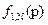відповідає вихідному стану P₁ , вказує суму максимального доходу, а вся таблиця в цілому дає змогу оцінити вплив можливих змін вихідного стану на досяжний дохід.

Прямий хід методу ДП полягає в послідовному перегляді таблиць 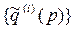{T_i (q,p)} у процесі руху від початку до кінця планованого періоду та фіксування оптимальних стратегій для вихідного і послідовно отримуваних станів:

Далі підраховується кількість звертань до таблиць при використанні ДП. Для побудови 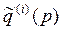та 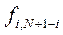до кожного з KL елементів таблиці R_j доводилося звертатися один раз, а всього – KL разів. Наявними є N етапів, а повне число звертань до цих таблиць становить NKL. Число звертань до таблиць {T_i(q,p)} становить (N-1)KL у процесі зворотного ходу, та ще (N-1) при прямому ході, що складає 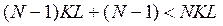. Звертання до раніше складених таблиць 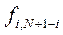у процесі зворотного ходу буде (N-1)KL, тобто повна кількість звертань не перевищить 3NKL. Розширення тієї ж розширеної, з варіацією початкового стану Р1, задачі ДП методом повного перебору вимагало б K(2N-1) L^N звертань. У типовому випадку 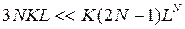, чи 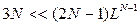, розв’язок конкретних задач ДП з врахуванням специфічних властивостей функції доходів (монотонність, випуклість і т.п.). Часто це дає змогу позбавитися від перебору на етапах зворотного ходу.

Цікавими також є проблеми ДП, пов’язані із задачами, для яких цільова функція має вигляд:

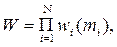
тобто W утворене добутком окремих показників. Прикладом можуть бути випадки, коли w_i – імовірність успіху на і-му етапі. Логарифмування W переводить цю задачу до вже розглянутого випадку з адитивним критерієм. Можливим є також пряме використання виразу для W, у цьому випадку на кожному кроці зворотного ходу максимізується добуток окремого показника даного кроку на виграш, отримуваний при всіх наступних кроках. Заміна оператора max на min дає змогу розв’язувати методом ДП задачі мінімізації (часу, витрат, імовірності відмови тощо).

Методи ДП застосовуються для оптимізації законів управління автоматичними системами, розрахунку тратторій, ціле розподіл, розв’язання задачі про призначення, оптимального резервування, вибору послідовності перевірок обладнання тощо. Задачі мережного планування, наприклад, знаходження критичного шляху, спираються на графовий варіант ДП. Застосування ДП до розв’язку задач з неоднорідними ресурсами ускладнено у зв’язку з експоненціальним, за числом типів ресурсів, зростанням об’єму перебору.