ЕЛЕМЕНТИ ТЕОРІЇ МНОЖИН
Основні означення теорії множин, операції
над множинами, властивості операцій над множинами
Під множиною прийнято розуміти сукупність об'єднаних за загальними ознаками різноманітних предметів.
Множини будемо позначати прописними латинськими буквами A,B,C, …, X, Y, Z, а елементи, що належать даним множинам - рядковими a, b, c, …, x, y, z…. Якщо a є елемент множини A, то пишуть 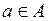 . Якщо a не є елементом множини A, пишуть
. Якщо a не є елементом множини A, пишуть 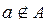 .
.
Множина, що не містить жодного елемента, називається порожньою множиною і позначається Æ.
Вихідна множина називається універсальною і позначаються U.
Якщо всі елементи множини A є також елементами множини B, то говорять, що А включається в B або A є підмножиною множини B і позначається 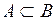 . Якщо
. Якщо 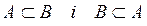 , то говорять, що A=B або A збігається з B.
, то говорять, що A=B або A збігається з B.
Діаграмами Ейлера-Венна називаються фігури, яки здійснюють зображення на площині множини и наочно демонструють властивості операцій над множинами. Прямокутник на площині
означатиме деяку універсальну множину, яке включає в себе усі розглянуті множини. Наприклад, 
Рисунок 1. Диграма Ейлера- Вена.
Об'єднанням двох множинA і B називається множина, яка складається з елементів, що входять хоча б в одну з даних множин, воно позначається 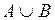 .
.
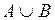 ={x: x
={x: x 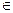 A або x
A або x 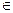 B },
B },
Відповідна диграма Ейлера- Вена:
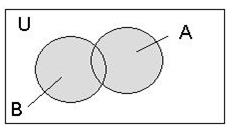
Рисунок 2. Об'єднання двох множин
Об'єднанням деякої сукупності множин  називається множина S, яка складається з усіх елементів, що входять хоча б в одну з множин
називається множина S, яка складається з усіх елементів, що входять хоча б в одну з множин 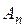 , і позначається
, і позначається  .
.
Перетином двох множинA іB називається множина, яка складається з усіх елементів, що належать як множині A, так і множині B, і позначається 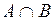 .
.
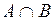 ={x: x
={x: x 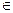 A і x
A і x 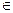 B }
B }
Про дві множини A і B говорять що вони не перетинаються, якщо їх перетин порожній.
Відповідна диграма Ейлера- Вена:
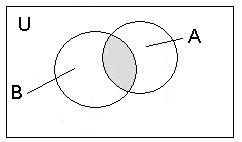
Рисунок 3.Перетин двох множин
Перетином деякої сукупності множин 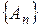 називається множина P, яка складається з усіх елементів, що входять у всі множини
називається множина P, яка складається з усіх елементів, що входять у всі множини 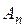 і позначається
і позначається 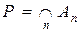 .
.
Різницею двох множинA іB називається множина, яка складається з усіх тих елементів множини A, що не належать множині B. Різниця позначається A \ B.
A \ B = {x: x 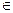 A і x
A і x  B }
B }
Відповідна диграма Ейлера- Вена:

Рисунок 4.Різниця двох множин
Прямим (або Декартовим) добутком двох множин A і B називається множина всіх пар
(x, y), де  . Декартів добуток множин A і B позначається
. Декартів добуток множин A і B позначається  .
.
Доповненням до множиниA називається множина 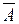 , що складається з елементів універсальної множини, U які не належать множині A, тобто
, що складається з елементів універсальної множини, U які не належать множині A, тобто  .
.
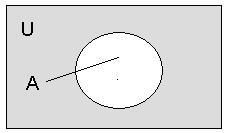
Рисунок5. Доповненням до множиниA
Операції над множинами мають такі властивості:
1. Комутативність: 
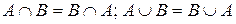 .
.
2. Асоціативність:  .
.
3. Дистрибутивність: 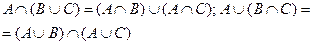 .
.
4. Закони де Моргана: 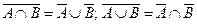 .
.
Приклад 1. Нехай 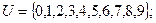
 . Знайти
. Знайти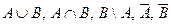 .
.
Розв’язок: об'єднання 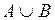 - це є множина S={x: x
- це є множина S={x: x 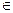 A або x
A або x 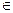 B }, Отже,
B }, Отже, 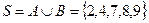 .
.
Перетин 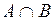 - це множина P= {x: x
- це множина P= {x: x 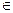 A і x
A і x 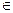 B }, Отже,
B }, Отже, 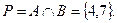
Різниця A\B - це множина R = {x: x 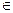 A і x
A і x  B }, тобто
B }, тобто 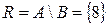 , аналогічно
, аналогічно 
Доповнення до множини A - це множина  ;
; 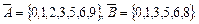
Прямий добуток  ={(4,2), (4,4),(4,7),(4,9),(7,2),(7,4),(7,7),(7,9),(8,2),(8,4),(8,7),(8,9)}.
={(4,2), (4,4),(4,7),(4,9),(7,2),(7,4),(7,7),(7,9),(8,2),(8,4),(8,7),(8,9)}.
Часто буває корисною рівність, що легко перевіряється
 . (1)
. (1)
Приклад 2. Довести рівність (1).
Для доведення рівності (1) необхідно показати:
1. 
2. 
Нехай 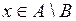 . З означення різниці множин випливає, що
. З означення різниці множин випливає, що 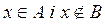 . Звідси випливає, що
. Звідси випливає, що 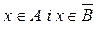 . Цей ланцюжок міркувань зручно записувати в такий спосіб:
. Цей ланцюжок міркувань зручно записувати в такий спосіб:
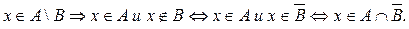
Тепер нехай  . З означення перетину випливає, що
. З означення перетину випливає, що 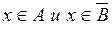 , а це еквівалентно такому:
, а це еквівалентно такому: 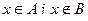 . Останнє означає, що
. Останнє означає, що 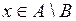 .
.
Стислий запис цього міркування виглядає так:
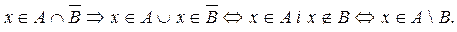
Рівність доведена.
Лекція 3. БІНАРНІ ВІДНОШЕННЯ
Бінарним відношенням R на множині A називається будь-яка підмножина R декартова добутку A 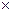 A . Наприклад, А = {1,2,3}, A
A . Наприклад, А = {1,2,3}, A 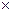 A = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)},
A = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3)},
R - підмножина пар, де перша цифра – непарная. Належність пари (x, y) відношенню R позначають 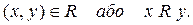
Способи завдання відношень.
1. Аналітичний.
Для завдання R на множині А потрібно указати всі пари (x,y) 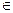 A
A 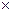 A, які містятьсяв R, тобто для яких виконується R.
A, які містятьсяв R, тобто для яких виконується R.
2. Завдання матрицею.
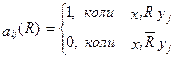
1. Завдання графом.
Елементи множини А відповідають вершинам графа, а 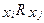 відповідає дуги
відповідає дуги  .
.
Операції над відношеннями.
Нехай  і
і 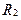 - відношення. Перетин
- відношення. Перетин  відповідає перетину множин, об’єднання
відповідає перетину множин, об’єднання  -
-
об’єднанню множин.
Повернутим до відношення R називають відношення 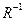 , яке визначається умовою
, яке визначається умовою
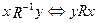
Якщо R – відношення «більше», то 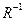 - відношення «менше». Дійсно, коли x<y
- відношення «менше». Дійсно, коли x<y 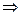 y<x і навпаки.
y<x і навпаки.
Властивості відношень.
Бінарне відношення R називається відношенням еквівалентності, якщо воно має властивості:
Рефлексивності -  Симетричності -
Симетричності - 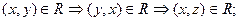
Транзитивності - 
Бінарне відношення R називається відношенням порядку, якщо воно має властивості: рефлексивності, транзитивності, антисиметричності - 
Приклад 3. Нехай N - множина натуральних чисел. На множині N x N визначимо R у такий спосіб: 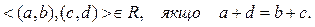 Показати, що R є відношенням еквівалентності.
Показати, що R є відношенням еквівалентності.
Розв’язок.Покажемо, що виконується властивість рефлексивності, тобто 
a+b = a+b – очевидно виконується.
Симетричність: 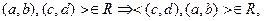 тобто з рівності a+d=b+c випливає c+b=d+a - очевидно виконується.
тобто з рівності a+d=b+c випливає c+b=d+a - очевидно виконується.
Транзитивність: 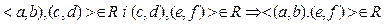 , тобто з рівності
, тобто з рівності
a + d = b + c; c+ f = d + e випливає рівність a + f = b + e. Додаючи вихідні рівності, одержимо
a + d + c + f = b + d + c + e, тобто a + f = b + e.
Таким чином, дане бінарне відношення є відношенням еквівалентності.
Розбиття множини на класи
Розбиттям множини на класи називається представлення цієї множини у виді суми не порожніх її підмножин, що не перетинаються.
Множина  розбита на класи
розбита на класи  якщо
якщо 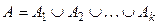 , де
, де 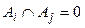 ,
, 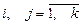 ,
, 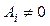 ,
, 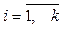 . Звичайно доводиться мати справу з розбиттями, побудованими на базі тієї чи іншої ознаки, за якою елементи множини
. Звичайно доводиться мати справу з розбиттями, побудованими на базі тієї чи іншої ознаки, за якою елементи множини 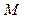 об’еднуються у класи. Наприклад, множина усіх трикутників на площині можна розбити на класи рівних між собою чи на класи рівновеликих трикутників. Ознаки, за якими елементи множини розбиваються на класи, можуть бути найрізноманітнішими, але все ж така ознака не цілком довільна. Припустимо, наприклад, що ми захотіли розбити всі дійсні числа на класи, включаючи число b в той же клас, що і число a, у тім і тільки тім випадку, якщо
об’еднуються у класи. Наприклад, множина усіх трикутників на площині можна розбити на класи рівних між собою чи на класи рівновеликих трикутників. Ознаки, за якими елементи множини розбиваються на класи, можуть бути найрізноманітнішими, але все ж така ознака не цілком довільна. Припустимо, наприклад, що ми захотіли розбити всі дійсні числа на класи, включаючи число b в той же клас, що і число a, у тім і тільки тім випадку, якщо 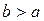 . Ясно, що таким шляхом ніякого розбиття одержати не можна, тобто якщо
. Ясно, що таким шляхом ніякого розбиття одержати не можна, тобто якщо 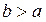 , то
, то 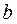 слід зарахувати в той же клас, що і
слід зарахувати в той же клас, що і 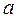 , разом з тим
, разом з тим 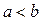 , тобто число a не можна включити в той же клас, що і b. Крім того, оскільки a не більше, ніж саме
, тобто число a не можна включити в той же клас, що і b. Крім того, оскільки a не більше, ніж саме 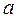 , то a не повинно потрапити в один клас із самим собою.
, то a не повинно потрапити в один клас із самим собою.
Для того, щоб відношення (ознака) дозволяло розбити множину M на класи, необхідно і достатньо, щоб воно було відношенням еквівалентності. Розбиття множини на класи проілюструємо за допомогою діаграми Ейлера - Венна. З Рисунка 6 видно, що вийшло вісім неперетинних підмножин. Виразимо ці підмножини через операції перетину і доповнення.
1. 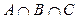 5.
5. 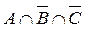
2. 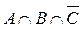 6.
6. 
3. 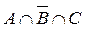
 7.
7. 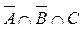
4. 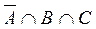 8.
8. 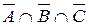
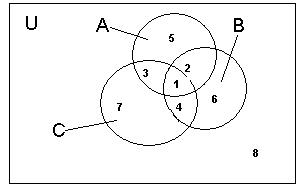
Рисунок 6. Розбиття множини на класи
Множина 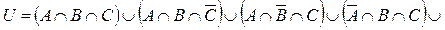
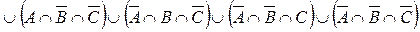
Лекція 4,5. ЕЛЕМЕНТИ КОМБІНАТОРИКИ
Загальні правила комбінаторики
До загальних правил комбінаторики відносяться: правило множення, правило додавання, формула включень та виключень.
Правило множення. Якщо об'єкт A можна вибрати m способами і якщо після кожного такого вибору об'єкт B можна вибрати n способами, то вибір пари (A, B) можна здійснити m x n способами.
Правило додавання. Якщо деякий об'єкт А можна вибрати m способами, а інший об'єкт В можна вибрати n способами, то вибір “або А, або В” можна здійснити m + n способами.
При використанні правила додавання необхідно стежити, щоб жодний із способів вибору об'єкта А не збігався з яким-небудь способом вибору об'єкта В.
Правила множення і додавання справедливі для будь-якого скінченого числа об'єктів.
Дата добавления: 2015-05-30; просмотров: 2442;
