Геометричний спосіб

На площині кожному елементу множини A довільним способом ставиться у відповідність точка.

Дві точки площини з'єднують лініями, якщо заданий вихідний і відображенний елементи.

Матричний спосіб

Якщо граф містить n вершин, то йому ставиться у відповідність матриця суміжності порядку n´n, рядкам і стовпчикам якої ставляться у відповідність вершини графа, а елемент матриці, що стоїть на перетині i-го рядка і j-го стовпчика, дорівнює одиниці, якщо x_i і х_j вершини суміжні, і дорівнює нулю в противному випадку.

Якщо граф містить n вершин і m ребер, то йому ставиться у відповідність матриця інциденцій порядку n´m, рядки якої відповідають вершинам, а стовпчики - ребрам; елемент матриці, що стоїть на перетині i-го рядка і j-го стовпчика, дорівнює 1, якщо x_i інцидентна ребру v_j, і дорівнює 0 в противному випадку. Елемент матриці, що стоїть на перетині i-го рядка і j-го стовпчика, може дорівнювати 1, якщо вершина x_i є кінцем дуги v_j, і дорівнює 1, якщо вершина x_i є початком дуги v_j або v_j - петля при x_i, і дорівнює 0, якщо вершина x_i і дуга v_j не інцидентні.

Приклад 9. Для заданого аналітично графа G (X, F): X = {x₁, x₂, x₃, x₄, x₅}; F(x₁) = {x₁, x₃, x₅};

F(x₂) = Æ; F(x₃) = {x₁, x₂, x₅}; F(x₄) = {x₁}; F(x₅) = {x₁, x₂, x₃, x₄, x₅}. Знайти геометричне і матричне зображення графа G (X, F).

Геометричне зображення гpaфа G (X, F), наведене на Рисунке 10, де вершини графа позначені точками x_i (i = 1, 2, 3, 4, 5), а дуги v_j (j = 1¸11) зображені напрямленими відрізками.

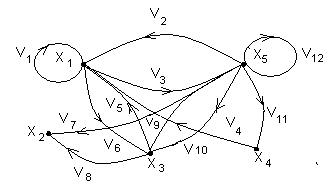
Рисунок 8.

Геометричне зображення графа G (X, F)

Матричне зображення вищенаведеного графа.

Матриця суміжності: Матриця інциденцій:

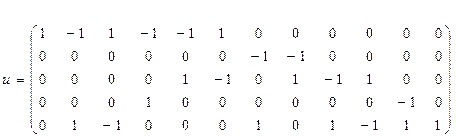
Лекція 12. ОПЕРАЦІЇ НАД ГРАФАМИ