Лекція 14.15. ПРИКЛАД ЗАСТОСУВАННЯ АЛГОРИТМА ФОРДА_ФАЛКЕРСОНА
Приклад 11. Розглянемо граф, зображений на Рисунке 12. Потрібно знайти максимальний потік від х1 до x9.
Розв’язок. Як початковий візьмемо потік із нульовими значеннями на всіх дугах xij = 0, "ij.
Пропускні спроможності дуг qij зазначені на Рисунке 12.
Крок 1. Припишемо вершині xi позначку (+ x1, ¥).
Крок 2.а) множина непозначених вершин: {xj|xj Î F(x1), x1j < q1j} = {x1, x4}.
Вершині x2 приписується позначка (+x1, min (¥, q12 - x12)) = (+x1, min (¥, 14-0) = (+x1, 14).
Вершині x4 приписується позначка (+x1, min (¥, q14 - x14)) = (+x1, min (¥, 23-0) = (+x1, 23).
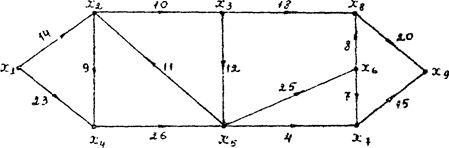
Рисунок 12. Вихідний граф.
б) множина непозначених вершин: {xj|xj Î F-1(x1), xj1 > 0} = Æ.
Отже, x1 позначена і переглянута, x2 і x4, позначені і не переглянуті, а всі інші вершини не позначені.
Повторюємо крок 2, переглядаючи вершину x2 (вершини переглядаються в порядку зростання їхніх номерів). Множина непозначених вершин:
a) {xj|xj Î F(x2), x2j < q2j} = {x3}.
Позначка для x3: (+x2, min (14, q23 - x23)) = (+x1, min (14, 10-0) = (+x2, 10).
б) Множина непозначених вершин
{xj|xj Î F-1(x2), xj2 > 0} = Æ.
Тепер вершини х1 і х2 позначені і переглянуті, а x3, x4 позначені і не переглянуті.
Переглядаємо вершину x3.
а) множина непозначених вершин: {xj|xj Î F(x3), x3j < q3j} = {x5, x8}.
Для x5 позначкою є (+x3, min (10, 12-0)= (+x3, 10),
для x8 позначкою є (+x3, min (10, 18-0) = (+x3, 10).
Переглядаючи x4, ніяких позначок розставити не можна, тому що всі суміжні з x4 вершини вже позначені. Переглядаючи x5, одержимо такі позначки:для x6 - (+x5, min (10, 25-10) = (+x5, 10);
для x7 - (+x5, min (10, 4-0) = (+x5, 4).
Переглядаючи x7 одержимо позначку для x9 - (+x5, min (4, 15-0) = (+x5, 4).
Переходячи до кроків 4 і 5, отримаємо
x = x9 - відповідна позначка (+x7, 4). Потік x79 змінюємо, додаючи d(x9) = 4, x79 = 0 + 4 = 4;
x = x7 - відповідна позначка (+x5, 4). Потік x57 = 0 + 4 = 4;
x = x5 - відповідна позначка (+x3,10). Потік x35 = 0 + 4 = 4;
x = x2 - відповідна позначка (+х1, 14). Потік x12 = 0 + 4 = 4.
Всі інші значення потоків залишилися рівними нулю. Потік наприкінці кроку 5 і позначки вершини до їхнього стирання на кроці 6 показані на Рисунок 13а. Стираючи позначки у вершин і повертаючись до кроку 1 для другого проходу, одержимо такі нові позначки:
для x1 - (+x1,¥);
для x2 - (+x1, min (¥, 14-4) = (+x1, 10);
для x3 - (+x1, min (¥, 23-0) = (+x2, 23). Вершина x1 позначена і переглянута. Переглядаючи вершину x2, одержимо позначку
для x3 - (+x2, min (10, 10-4)) = (+x2, 6). Вершина x2 позначена і переглянута.
Переглядаючи вершину x3, одержимо позначки: для x5 - (+x3, min (6, 12-4)) = (+x3, 6);
для x8 - (+x3, min (6, 18-0)) = (+x3, 6).
Вершина x3 позначена і переглянута. Переглядаючи вершину x5, одержимо позначки:
для x6 - (+x5, min (6, 25-0)) = (+x5, 6). Вершина x5 позначена і переглянута.
Переглядаючи вершину x6, знаходимо, що позначкою для x7 будет (+x6, min (6, 7-0)) = (+x6, 6).
Тепер вершина x6 позначена і переглянута. Позначкою для x9 : (+x7, min (6, 15-4)) = (+x7, 6).
Кроки 4 і 5. Нові потоки збільшилися в такий спосіб:
x79 = 4 + 6 = 10; x67 = 0 + 6 = 6; x56 = 0 + 6 = 6;
x35 = 4 + 6 = 10; x23 = 4 + 6 = 10; x12 = 4 + 6 = 10.
Всі інші значення потоку не змінилися. Новий потік і позначки вершин до стирання показані на Рисунок 13б.
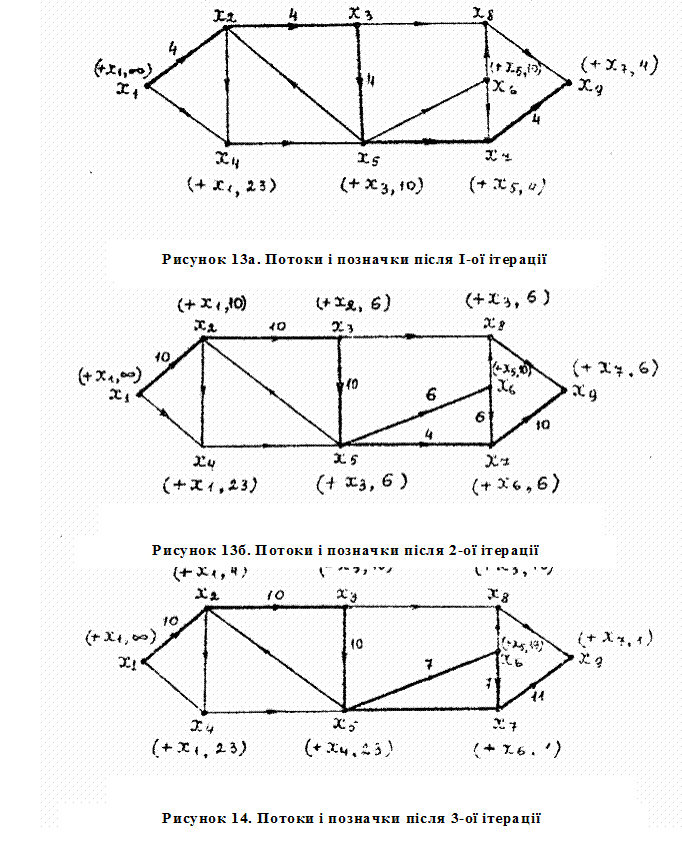
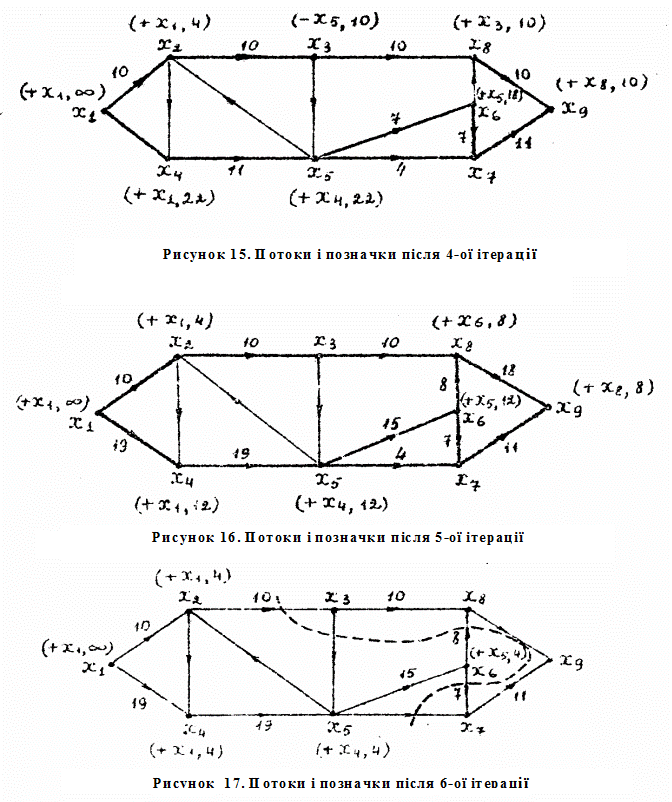
Аналізуючи всі етапи визначення потоків, одержуємо після кожного проходу алгоритма потоки і позначки, зображені послідовно на Рисунках 14-17. Алгоритм закінчує роботу, коли тільки вершина x6 може бути позначена. Розріз графа зображен на Рисунке 17 пунктиром . Множина  містить позначені вершини, а множина
містить позначені вершини, а множина 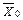 - непозначені вершини. Потік, що відповідає дугам (x2, x3), (x3, x6), (x6, x7), (x6, x8), (x5, x7) є максимальним із значенням
- непозначені вершини. Потік, що відповідає дугам (x2, x3), (x3, x6), (x6, x7), (x6, x8), (x5, x7) є максимальним із значенням
10 + 0 + 8 + 7 + 4 = 29.
Лекція 16,17. ЗАДАЧА ПОШУКУ НАЙКОРОТШОГО (КРИТИЧНОГО) ШЛЯХУ МІЖ ДВОМА ЗАДАНИМИ ВЕРШИНАМИ S И t (cij ³ 0)
Нехай l(xi) - позначка вершини xi.
1. Приcвоєння початкових значень
Крок 1. Покласти l(s) = 0 і вважати цю позначку постійною.
Покласти для всіх l(xi) = ¥ і вважати ці позначки тимчасовими. Покласти p = s.
2. Відновлення позначок
Крок 2. Для всіх xiÎF(р), позначки яких тимчасові, змінити позначки у відповідності з таким виразом:
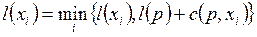
Перетворення позначки в постійну
Крок 3. Серед усіх вершин із тимчасовими позначками знайти таку, для якої
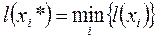 .
.
Крок 4. Вважати позначку вершини xi* постійною і покласти p = xi*.
Якщо p = t, то l(p) є довжиною найкоротшого шляху. Якщо p ¹ t, то перейти до кроку 2.
Приклад 35. Розглянемо граф, зображений на Рисунке 18 , де кожне неорієнтоване ребро розглядається як пару протилежно орієнтованих дуг рівної ваги. Матриця С ваг приведена нижче.
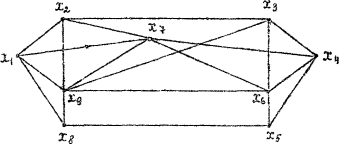
Рисунок 18. Вихідний граф.
Матриця ваг
| С = | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | |
| x1 | ||||||||||
| x2 | ||||||||||
| x3 | ||||||||||
| x4 | ||||||||||
| x5 | ||||||||||
| x6 | ||||||||||
| x7 | ||||||||||
| x8 | ||||||||||
| x9 |
Крок 1. l(x1) = 0 - позначка постійна.
l(x1) = р, "xi ¹ xi
p = xi
Перша ітерація
Крок 2. F(p) = {x2, x7, x8, x9} множина вершин, в які є дуга з x1.
Позначки l(x2), l(x7), l(x8), l(x9) - тимчасові і рівні ¥.
Обновляємо позначку вершини x2, для цього находим
min {l(x2), l(p) + c(p, x2)}. Тому що l(x2) = ¥, а l(p) = 0, с12 = 10, то одержуємо min {¥, 0+10}= 10, виходить, l(x2) = 10.
Аналогічно знаходимо
l(x7) = min {¥, 0+3}= 3;
l(x8) = min {¥, 0+6}= 6;
l(x9) = min {¥, 0+12}= 12.
Крок 3. Знаходимо min {l(xi)}, тобто
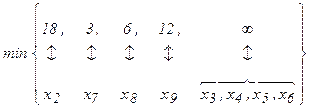 відповідає x7
відповідає x7
Крок 4. x7 одержує постійну позначку l(x7) = 3; p = x7.
Крок 5. Не всі вершини мають постійну позначку, тому переходимо до кроку 2. Позначки на початку другої ітерації показані на Рисунке 19. Із знаком + показані постійні позначки.
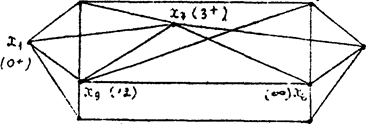
Рисунок 19. Перша итерація.
Друга ітерація
Крок 2. F(p) = F(x7) = {x2, x4, x6, x9} - усі позначки тимчасові.
Обновляємо позначку вершини x2. З огляду на те, що l(x2) = 10, l(p) = 3,
C72 = 2, знаходимо min {10, 3+2}= 5, тобто l(x2) = 5.
Аналогічно l(x4) = min {¥, 3+4}= 7;
l(x6) = min {¥, 3+14}= 17;
l(x9) = min {12, 3+24}= 12.
Крок 3. Знаходимо min {l(xi)}, тобто
 відповідає x2
відповідає x2
Крок 4. x2 одержує постійну позначку l(x2) = 5; p = x2.
Крок 5. Перейти до кроку 2.
Обчислення по кожній ітерації зручно звести в таблицю, наведену на Рисунок 20
| x1 | x2 | x3 | х4 | x5 | x6 | x7 | x8 | х9 | |
| х1+ | 0+ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ | ¥ |
| х7+ | ¥ | ¥ | ¥ | ¥ | 3+ | ||||
| х2+ | 5+ | ¥ | ¥ | ||||||
| х8+ | ¥ | 6+ | |||||||
| х4+ | 7+ |
Рисунок 20. Сводная таблиця всіх итерацій.
Перший рядок таблиці відповідає початковим позначкам вершин. Показані зліва в таблиці вершини зі знаком + одержують постійні позначки, а числа зі знаком + у рядку таблиці відповідають min{l(xi)}. Після першої ітерації постійну позначку одержала вершина x7, а min{l(xi)} = 3. Після того, як вершина x7 одержала постійну позначку, числа в стовпчику, що відповідає х7 залишаються незмінними.
На четвертій ітерації постійну позначку одержує х4, тобто р = х4, а х4 відповідає стокові t. Таким чином, алгоритм закінчує роботу, довжина найкоротшого шляху дорівнює
l(p) = l(x4) = 7.
Для знаходження найкоротшого шляху використаємо співвідношення:
l(xi') + c(xi', xi) = l(xi), (*)
xi' - вершина, що безпосередньо передує вершині xi у найкоротшому шляху від S до xi. Якщо існує декілька найкоротших шляхів від S до якоїсь іншої вершини, то при деякій фіксованій вершині xi' співвідношення (*) буде виконуватися більш ніж для однієї вершини xi. У цьому випадку вибір може бути або довільним (якщо потрібний якийсь один найкоротший шлях між S і xi), або таким, що розглядаються всі дуги, які входять в якийсь із найкоротших шляхів.
Знайдемо найкоротший шлях від x1 до x2. Для цього знаходимо вершину х2' із співвідношення:
l(x2') + c(x2', x2) = l(x2) = 5.
У стовпчику, x2 матриці С, і в останньому рядку таблиці (див. Рисунок 20) знаходимо числа, сума яких дорівнює 5. У стовпчику x2 матриці С містяться числа 10, 18, 2, 13. Потрібно взяти число 2, що відповідає вершині x7
l(x7') + c(x7', x7) = 3 + 2 = 5,
тобто вершиною, що задовольняє співвідношенню (*), є x7.
Поклавши xi = x7, знаходимо вершину безпосередньо передуючу x7 у найкоротшому шляху від x1 до x2. Вершина x7', повинна задовольняти співвідношення:
l(x7') + c(x7', x7) = 3.
У стовпчику x7 матриці С містяться числа 3, 2, 4, 14, 24. Можна брати або 2, або 3. Візьмемо число, рівне 2, йому відповідає вершина x2, l(x2) + c(x2, x7) = 2 + 5 ¹ 3, виходить, x2 не задовольняє співвідношення (*). Залишається вершина x1, l(x1) + c(x1, x7) = 0 + 3 = 3. Таким чином, єдиною вершиною яка задовольняє співвідношення (*), є x1. Отже, найкоротшим шляхом від x1 до x2 є шлях (x1, x7, x2).
Знаходимо найкоротший шлях від x1 до x3, відзначимо, що l(x3) = 23.
У стовпчику x3 матриці С містяться числа 18, 25, 20. Придатним числом є 18, якому відповідає x2.
l(x2) + c(x2, x3) = 5 + 18 = 23 = l(x3).
Виходить, найкоротший шлях від x1 до x3 - це шлях (x1, x7, x2, x3).
Аналогічно можна знайти найкоротші шляхи від вершини x1 до будь-якої вершини мережного графа. Ці дуги зображені на Рисунке 21 жирними лініями. З Рисунку 21 очевидно, що найкоротший шлях від x1 до x4 - це шлях (x1, x7, x4).
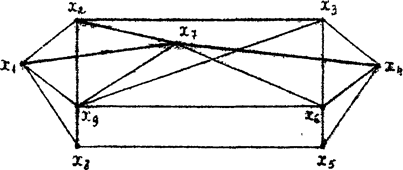
Рисунок 21. Найкоротший шлях.
Для того, щоб знайти критичний шлях у шляховому графіку, необхідно внести такі зміни на кроці 2 і кроці 3.
Крок 1. Покласти l(s) = 0 і вважати цю позначку постійною.
Покласти для всіх l(xi) = - ¥ і вважати ці позначки тимчасовими. Покласти p = s.
Крок 2. l(xi) = max {l(xi), l(p) + c(p, xi)}
Крок 3. l(xi*) = max {l(xi)} тобто замість мінімальних значень брати максимальні, а замість матриці вартостей С = (сij) - розглядати матрицю часу переходу від i-ой до j-ой роботи T = (tij).
Дата добавления: 2015-05-30; просмотров: 1056;
