Принцип Гюйгенса — Френеля

Явления интерференции света во всем их многообразии служат убедительнейшим доказательством волновой природы световых процессов. Однако окончательная победа волновых представлений была невозможна без истолкования с волновой точки зрения фундаментального и хорошо подтвержденного опытом закона прямолинейного распространения света.

Волновые представления в той первоначальной форме , в которой их развивал Гюйгенс («Трактат о свете», 1690), не могли дать удовлетворительного ответа на поставленный вопрос. В основу учения о распространении света Гюйгенсом положен принцип, носящий его имя. Согласно представлениям Гюйгенса, свет, по аналогии со звуком, представляет собой волны, распространяющиеся в особой среде — эфире, занимающем все пространство, в частности заполняющем собой промежутки между частицами любого вещества, которые как бы погружены в океан эфира. С этой точки зрения естественно было считать, что колебательное движение частиц эфира передается не только той частице, которая лежит на «пути» светового луча, т. е. на прямой, соединяющей источник света L, (рис. 1.1) с рассматриваемой точкой А, но всем частицам, примыкающим к А, т. е. световая волна распространяется из А во все стороны, как если бы точка А служила источником света. Поверхность, огибающая эти вторичные волны, и представляет собой поверхность волнового фронта. Для случая, изображенного на рис. 1.1, эта огибающая (жирная дуга) представится частью шаровой поверхности с центром в L, ограниченной конусом, ведущим к краям круглого отверстия в экране МN. Принцип Гюйгенса позволил разъяснить вопросы отражения и преломления света, включая и сложную проблему о двойном лучепреломлении; но задача о прямолинейном распространении света по существу решена не была, ибо она не была поставлена в связь с явлениями отступления от прямолинейности, т. е. с явлениями дифракции.

Причина лежит в том, что принцип Гюйгенса в его первоначальной форме был принципом, областью применения которого являлась область геометрической оптики. Выражаясь языком волновой оптики, он относился к случаям, когда длину волны можно было считать бесконечно малой по сравнению с размерами волнового фронта. Поэтому он позволял решать лишь задачи о направлении распространения светового фронта и не затрагивал по существу вопроса об интенсивности волн, идущих по разным направлениям. Этот недостаток воспол нил Френель, который вложил в принцип Гюйгенса физический смысл, дополнив его идеей интерференции волн. Благодаря этому огибающая поверхность элементарных волн, введенная Гюйгенсом чисто формально, приобрела ясное физическое содержание как поверхность, где благодаря взаимной интерференции элементарных волн результирующая волна имеет заметную интенсивность.

Модифицированный таким образом принцип Гюйгенса—Френеля становится основным принципом волновой оптики и позволяет исследовать вопросы, относящиеся к интенсивности результирующей волны в разных направлениях, т. е. решать задачи о дифракции света (см. ниже). В соответствии с этим был решен вопрос о границах применимости закона прямолинейного распространения света, и принцип Гюйгенса—Френеля оказался применимым к выяснению закона распространения волн любой длины.

Для отыскания интенсивности (амплитуды) результирующей волны нужно, согласно Френелю, следующим образом формулировать принцип Гюйгенса.

Окружим источник L воображаемой замкнутой поверхностью S любой формы (рис. 1.2). Правильное значение интенсивности (амплитуды) возмущения в любой точке В за пределами S может быть получено так: устраним L, а поверхность S будем рассматривать как светящуюся поверхность, излучение отдельных элементов которой, приходя в В, определяет своей совокупностью действие в этой точке. Излучение каждого элемента ds поверхности S надо представлять себе как сферическую волну (вторичная волна), которая, приносит в точку В колебание:

,

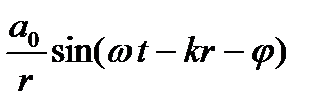где а₀ определяется амплитудой, а φ — фазой действительного колебания, дошедшего от L до элемента ds, находящегося на расстоянии r от точки В. При этом размеры элемента ds предполагаются настолько малыми, что φ и r для любой части его можно считать имеющими одни и те же значения. Другими словами, каждый элемент ds рассматривается как некоторый вспомогательный источник, так что амплитуда a₀, пропорциональна площади ds.

Постулат Френеля, позволяющий определить a₀ и φ через амплитуду и фазу дошедшего до ds колебания, представляет собой некую гипотезу, пригодность которой может быть установлена сравнением делаемых с ее помощью заключений с результатами опыта.

Так как фазы всех вспомогательных источников определяются возмущением, идущим из L, то они строго согласованы между собой, и, следовательно, вспомогательные источники когерентны. Поэтому вторичные волны, исходящие из них, будут интерферировать между собой. Их совокупное действие в каждой точке может быть определено как интерференционный эффект, и следовательно, идея Гюйгенса о специальной роли огибающей перестает быть допущением, а должна явиться лишь следствием законов интерференции. Согласно приведенному выше постулату Френеля вопрос о вспомогательных источниках, заменяющих L, решается однозначно, как только выбрана вспомогательная поверхность S. Выбор же этой поверхности вполне произволен; поэтому для каждой конкретной задачи се следует выбрать наивыгоднейшим для решения способом. Если вспомогательная поверхность S совпадает с фронтом волны, идущей из L. (представляет собой сферу с центром в S), то все вспомогательные источники будут иметь одинаковую фазу. Если же выбор S сделан иначе, то фазы вспомогательных источников не одинаковы, но источники, конечно, остаются когерентными.

В том случае, когда между источниками L и точкой наблюдения имеются непрозрачные экраны с отверстиями, действие этих экранов может быть учтено следующим образом. Мы выбираем поверхность S так, чтобы она всюду совпадала с поверхностью экранов, а отверстия в них затягивала произвольным образом, выбранным в зависимости от разбираемой проблемы. На поверхности непрозрачных экранов амплитуды вспомогательных источников должны считаться равными нулю; на поверхности же, проходящей через отверстия экранов, амплитуды выбираются в согласии с постулатом Френеля, т. е. так, как если бы экран отсутствовал. Таким образом, предполагается, что материал экрана не играет, роли, если только экран не прозрачен.

Вычисляя результаты интерференции элементарных волн, посылаемых вспомогательными источниками, мы приходим к значению амплитуды (интенсивности) в любой точке В, т. е. определяем закономерность распространения света. Результаты этих вычислений подтверждаются данными опыта. Таким образом, по методу Гюйгенса—Френеля удается получить правильное решение вопроса о распределении интенсивности света как в случае свободного распространения световых волн (прямолинейное распространение), так и в случае наличия задерживающих экранов (дифракция).

Первой задачей, которую должен был рассмотреть Френель, выдвинув новую формулировку принципа Гюйгенса, явилась задача о прямолинейном распространении света. Френель решил ее путем рассмотрения взаимной интерференции вторичных волн, применив чрезвычайно наглядный прием, заменяющий сложные вычисления и имеющий общее значение при разборе задач о распространении волн. Метод этот получил название метода зон Френеля.

Рассмотрим действие световой волны, испущенной из точки А, в какой-либо точке наблюдения В. Согласно принципу Гюйгенса-Френеля заменим действие источника А действием воображаемых источников, расположенных на вспомогательной поверхности S.

В качестве такой вспомогательной поверхности S выберем поверхность фронта волны, идущей из А (поверхность сферы с центром А, рис.. 1.3). Вычисление результата интерференции вторичных волн очень упрощается, если применить следующий указанный Френелем прием: для вычисления действия в точке В соединяем А с В и разбиваем поверхность S на зоны такого размера, чтобы расстояния от краев зоны до В отличались на λ/2 т. е.

M₁B – M₀B = M₂B – M₁B =M₃B – M₂B =…= λ/2

(см. рис. 1.3). Нетрудно вычислить размеры полученных таким образом зон. Из рис. 1.4 получаем для первой зоны

r²=a² – (a – x)² = (b+ λ/2)² – (b+x)²

Так как λ очень мало по сравнению с а пли b, то

,

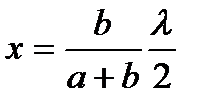и, следовательно, площадь сферического сегмента, представляющего первую, или центральную зону, есть:

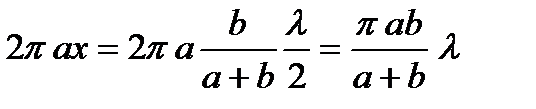
Для площади сегмента, представляющего две первые зоны, найдем значение 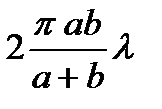, т.е. площадь второй зоны также равна 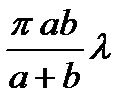. Практически ту же площадь будет иметь и каждая из всех последующих зон. Таким образом, построение Френеля разбивает поверхность сферической волны на равновеликие зоны, каждая из которых имеет площадь

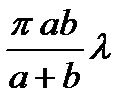
Для дальнейшего вычислении надо только принять во внимание, что действие отдельных зон на точку В тем меньше, чем больше угол φ между нормалью к поверхности зоны и направлением на В. Таким образом, действие зон постепенно убывает от центральной зоны (около М₀) к периферическим. Произвольное введение этого вспомогательного ослабляющего множителя есть один из недостатков метода Френеля.

Для получения окончательного результата можно рассуждать следующим образом: пусть действие центральной зоны в точке В выражается возбуждением колебания с амплитудой s₁, действие соседней зоны — колебанием с амплитудой s₂, следующей — с амплитудой s₃ и т. д. Как указано, действие зон постепенно (хотя и медленно) убывает от центра к периферии, так что s₁> s₂ > s₃ > s₄ и т. д.; действие п-й зоны s_n может быть очень малым, если п достаточно велико. Кроме того, благодаря выбранному способу разбивки на зоны легко видеть, что действия соседних зон ослабляют друг друга. Действительно, так как

M₁B – M₀B=λ/2 и M₂B – M₁B=λ/2

то воображаемые источники зоны М₀М₁ расположены на ½ λ ближе к В, чем соответственные источники зоны М₁М₂, так что посылаемые колебания дойдут до В в противоположных фазах. Таким образом, для точки В действие центральной зоны ослабится действием соседней зоны и т. д. Продолжая эти рассуждения, найдем, что окончательное значение амплитуды колебания, возбужденного в точке В всей совокупностью зон, т. е. всей световой волной, будет равно:

s=s₁ – s₂ + s₃ – s₄ + s₅ – s₆ +…=s₁ – (s₂ - s₃ ) – (s₄ – s₅) – (s₆ – s₇) – … (1.1)

Из условия s₁> s₂ > s₃ > s₄... следует, что все выражения в скобках положительны, так что s<s₁. Освещенность Е в точке наблюдения В пропорциональна квадрату результирующей амплитуды колебаний. Следовательно, Е ~ s² < s₁²|.

Итак, амплитуда s результирующего колебания, получающегося вследствие взаимной интерференции света, идущего к точке В от различных участков нашей сферической волны, меньше амплитуды, создаваемой действием одной центральной зоны. Таким образом, действие всей волны на точку В сводится к действию ее малого участка, меньшего, чем центральная зона с площадью 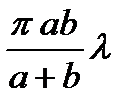. Длина световой волны λ весьма мала (для зеленого света λ = 5 • 10^-4 мм). Поэтому даже для расстоянии а и b порядка 1 м площадь действующей части волны меньше 1 мм². Следовательно, распространение света от A к В действительно происходит так, как если бы световой поток шел внутри очень узкого канала вдоль АВ, т. е. прямолинейно.

Это не значит, однако, что если мы поместим на линии АВ любой небольшой непрозрачный экран, то до точки В свет не дойдет; ведь внесение такого экрана, который прикроет, например, первую зону, нарушит правильность наших рассуждений. В этом случае выпадет первый член знакопеременного ряда (1.1), и теперь окажется, что s < |s₂ | и т. д., т. е. s меньше модуля s_m, где т — номер первой открытой у края экрана зоны. Если т не велико, например, т < 10, то освещенность в точке наблюдения В на оси экрана останется почти такой же, как и в его отсутствие. Но если маленький экранчик имеет неровные края с зазубринами, сравнимыми с шириной зоны Френеля, по которой проходит этот край, то он существенно уменьшает интенсивность в точке наблюдения В.