Интерференция немонохроматических световых пучков

Как уже упоминалось интерференция немонохроматического света приводит к сложной картине, состоящей из совокупности максимумов и минимумов, соответствующих разным λ,. Если λ имеет все возможные значения, то согласно формуле h=mDλ/2l любой точке экрана (h) соответствует большая или меньшая интенсивность света данной длины волны. Следовательно, в любой части экрана имеется значительная освещенность. Если бы в нашем источнике различные длины волн были представлены с одинаковой интенсивностью, и приемное устройство было одинаково чувствительно ко всем длинам волн (например, идеально панхроматическая фотопластинка), то мы не могли бы обнаружить никаких следов интерференционной картины.

Для того чтобы такое обнаружение было возможно, необходимо, чтобы разнообразие длин волн было ограничено и не превышало некоторого спектрального интервала, заключенного между λ и λ + Δλ. Пользуясь формулой h=mDλ/2l, легко найти Δ λ. Действительно, интерференция не будет наблюдаться, если максимум т-го порядка для (λ + Δ λ) совпадет с максимумом (т + 1)-го порядка для λ. В этих условиях весь провал между соседними максимумами будет заполнен максимумами неразличимых длин волн нашего интервала (рис. 8.1). Условие неразличимости интерференционной картины: (т+1)λ =т (λ + Δ λ ), т.е. Δ λ, = λ /m, где т — целое число. Для того чтобы интерференционная картина при данных значениях Δλ. и λ, обладала высокой видимостью, приходится ограничиваться наблюдением интерференционных полос, порядок которых много меньше значения т = λ/Δλ.

Другими словами, чем выше порядок интерференции (т), который нужно наблюдать, тем уже должен быть спектральный интервал, еще допускающий наблюдение интерференции. Наоборот, чем менее монохроматичен свет, тем ниже порядки интерференции, доступные наблюдению.

Монохроматизацию света можно осуществить с помощью светофильтра или спектрального аппарата. При этом, конечно, безразлично, стоит ли монохроматизирующее приспособление перед интерферометром или после него. В первом случае мы уменьшаем спектральный интервал Δλ интерферирующего света. Во втором мы с помощью монохроматора устраняем из полученной интерференционной картины мешающие волны, так что на приемник (глаз, фотопластинка) падает уже упрощенная и различимая интерференционная картина. Роль такого «монохроматора» может играть и непосредственно наш глаз благодаря его способности к различению цветов: при наблюдении глазом мы легко отличаем максимум одного цвета от максимумов другого. Однако эта способность к различению у нашего глаза также ограничена, хотя и превосходит избирательную способность большинства физических приемников (фотоэлемент, фотопластинку и тем более вполне нейтральный термоэлемент). Особенно затруднительно для глаза различение оттенков при наличии непрерывного перехода. При этих условиях глаз вряд ли способен обнаружить различие, если λ меняется менее чем на несколько десятков (сто) ангстрем. Вооружив глаз светофильтром с узкой полосой пропускания или спектроскопом, мы получаем возможность наблюдать интерференцию при большей разности хода.

Порядок интерференции т связан с разностью хода интерферирующих световых пучков d₁ – d₂ и длиной волны λ соотношением т = (d₁ – d₂)/λ. Из проведенного выше обсуждения интерференции немонохроматического света следует, что разность хода, при которой исчезает интерференционная картина, определяется соотношением L= d₁ – d₂ = λ² / Δλ.

Эта величина называется длиной когерентности. Она определяется свойствами источника света либо применяемого монохроматора. Для того чтобы наблюдать интерференционную картину 'достаточной видимостью (например, с V 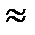0,1), необходимо обеспечить в интерференционной схеме условия, при которых максимальная разность хода интерферирующих световых пучков много меньше длины когерентности для применяемого источника

Опыт показывает, что при использовании в качестве источника света свечения разреженного газа длина когерентности для отдельных спектральных линий этого газа не превышает нескольких десятков сантиметров. Лазерные источники света позволяют наблюдать интерференцию при разности хода в несколько километров. Однако практический предел разности хода, при котором возможно наблюдение интерференции, ограничивается уже не длиной когерентности лазерных источников света, но трудностями создания стабильной интерференционной схемы подобных размеров и неоднородностью земной атмосферы.

Ранее указывалось, что волны, испускаемые атомами, сохраняют регулярность лишь в течение ограниченного интервала времени. Другими словами, в течение этого интервала времени амплитуда и фаза колебаний приблизительно постоянны, тогда как за больший промежуток времени и фаза, и амплитуда существенно изменяются. Часть последовательности колебаний, на протяжении которой сохраняется их регулярность, мы называли цугом волн или волновым цугом. Время испускания цуга волн называется длительностью цуга или временем когерентности. Пространственная протяженность цуга L (длина цуга волн) и время когерентности Т связаны очевидным соотношением L = Тс, где с —скорость света. Если, например, средняя длина цугов волн, излучаемых некоторым источником света, равна по порядку величины 1 см, то время когерентности для этого источника света составляет величину порядка 0,3·10^-10 с. Следовательно, в среднем через такие промежутки времени прекращается излучение одной регулярной последовательности волн, испускаемой источником света, и начинается излучение другого цуга волн с амплитудами, фазами и поляризацией, не связанными закономерно с соответствующими параметрами предшествующего волнового цуга.

Нетрудно понять, что длина когерентности и длина цуга волн совпадают. Действительно, если разность хода интерферирующих пучков становится больше длины цуга волн, то в данной точке интерференционного поля складываются волны, испущенные атомом в моменты времени, отличающиеся более чем на время когерентности. Но такие колебания не могут интерферировать. Следовательно, интерференция не может наблюдаться, если разность хода больше длины цуга, а максимальная разность хода, при которой интерференция еще наблюдается, т. е. длина когерентности, равна длине цуга.

Используя связь между длиной когерентности и шириной спектрального интервала Δλ, можно найти соотношение между Δλ, и временем когерентности Т

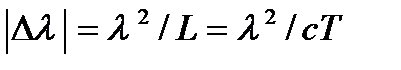
откуда, учитывая, что | Δλ| = с Δ ν/ ν ² , получаем

Δν Т=1

где Δν — ширина спектрального интервала в шкале частот.

Обратная пропорциональность между временем когерентности Т и отвечающей ему шириной спектрального интервала имеет весьма общий характер. Более строгая теория, учитывающая особенности случайных изменении фаз и амплитуд волны, приводит лишь к изменению числового значения в правой части соотношения.