Глава 20. Интерференция света

§ 20.1 Интерференция света. Принцип Гюйгенса. Опыт Юнга. Расчёт интерференционной картины от двух когерентных источников

Оптикой называют раздел физики, в котором изучаются свойства света.

Под светом в настоящее время понимают электромагнитное излучение, воспринимаемое человеческим глазом. Длина волн воспринимаемого электромагнитного излучения лежит в интервале от 0,38 до 0,76 мкм.

В физике часто называют светом и невидимые электромагнитные волны, лежащие за пределами этого интервала: от 0,01 до 340 мкм.

Первые представления о природе света возникли у древних греков и египтян. По мере изобретения и совершенствования различных оптических приборов (параболического зеркала, микроскопа, зрительной трубы) эти представления развивались и трансформировались. В конце XVII века возникли две теории света: корпускулярная (И. Ньютон) и волновая (Р. Гук и Х. Гюйгенс).

Согласно корпускулярной теории, свет представляет собой поток частиц (корпускул), испускаемых светящимися телами. Ньютон считал, что движение световых корпускул подчиняется законам механики.

Волновая теория, в отличие от корпускулярной, рассматривала свет как волновой процесс, подобный механическим волнам.

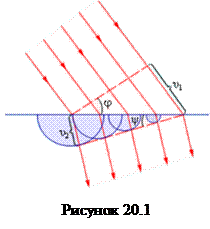В основу волновой теории был положен принцип Гюйгенса, согласно которому, каждая точка волновой поверхности, которой достигла в данный момент волна, является центром вторичных волн, их внешняя огибающая будет волновой поверхностью в последующий момент времени( рис.20.1).

Наиболее ярко волновые свойства света проявляются в явлениях интерференции и дифракции.

Интерференцией света называется сложение двух (или нескольких) когерентных световых волн, в результате чего в одних точках пространства происходит усиление интенсивности света, а в других – ослабление.

Явление интерференции проще всего наблюдать в случае механических волн. Например, на поверхности воды, когда поблизости колеблются два поплавка (рис.20.2). Каждый из поплавков является источником волн. Волны эти свободно проходят одна сквозь другую, как будто другой волны не существует.

Когерентными называются волны одинаковой частоты, разность фаз которых не изменяется.

Когерентность есть необходимое условие интерференции волн. Когерентные волны можно получить от одного источника.

Открытие и исследование интерференции света связаны с именем замечательного английского ученого Т. Юнга.

В 1801 г. Юнг высказывает очень важное предположение, со­гласно которому «ощущение различных цветов зависит от различной частоты колебаний, возбуждаемых светом в сетчатке» (так называемая «третья гипотеза» Юнга).

Вскоре он приходит к выводу, что световые волны могут усиливать и ослаблять друг друга, и в науке появляется новый термин — «интерференция».

Для подтверждения своей теории Юнг проводит классический опыт по интерференции света, описание которого впоследствии вошло во все учебники физики.

В опыте Юнга свет от Солнца падал на экран с узкой щелью S (рис. 20.3). Прошедшая через эту щель световая волна падала затем на второй экран уже с двумя щелями S₁ и S ₂. Когда в область перекрытия световых волн, идущих от S₁ и S₂, помещался третий экран, то на нем появлялись параллельные светлые и тёмные интерференционные полосы.

Для световых волн, так же как и для любых других, справедлив принцип суперпозиции. Так как свет имеет электромагнитную природу, то применение этого принципа означает, что результирующая напряжённость электрического (магнитного) поля двух световых волн, проходящих через одну точку, равна векторной сумме электрических (магнитных) полей каждой из волн в отдельности.

При сложении плоских когерентных волн амплитуда результирующих колебаний определяется формулой

А²=А₁²+А₂² +2А₁А₂cos(φ₂ – φ₁) (20.1)

((φ₂ – φ₁) – разность фаз слагаемых волн).

Анализируя уравнение (20.1), делаем выводы:

Если φ₂ – φ₁ = 0, 2π; 4 π;….;…2k π, где k = 0,1,2,3, …, то

cos(φ₂ – φ₁) =1 и А=А₁+А₂ (20.2)

Если φ₂ – φ₁ = π, 3π, 5π,…; (2k-1)π, где k = 0,1,2,3, …, то

cos(φ₂ – φ₁) =-1 и А=|А₁-А₂| (20.3)

В первом случае происходит усиление колебаний, во втором – ослабление. Если при этом А₁=А₂, то А_min = 2А₁, А_min =0. В последнем случае происходит гашение света светом.

Обычно эти условия формулируются не через разность фаз φ₂ – φ₁ , а через разность хода волн Δ. Разность хода Δравна разности расстояний, которые проходят волны от источников.

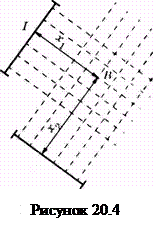Пусть одна из интерферирующих волн проходит путь х₁ со скоростью υ₁ в среде с показателем преломления 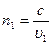, а другая – путь х₂ со скоростьюυ₂ в среде с показателем преломления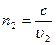

(рис.20.4).

При наложении волн разность фаз

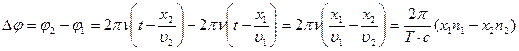
Учитывая, что длина волны в вакууму λ= c T,

а L₁=x₁n₁, L₂=x₂n₂,

L=x n (20.4)

- оптическая длина пути, имеем

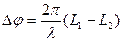(20.5)

(величина Δ = L₁ - L₂ - оптическая разность хода). (20.6)

Тогда 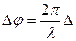или

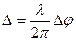(20.7)

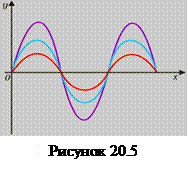Условие максимума: колебания в данной точке пространства будут усиливаться, если волны приходят в неё в одинаковой фазе и амплитуда будет максимальной (рис. 20.5). Такое возможно при условии, если разность хода световых волн равна чётному числу полуволн или целому числу волн:

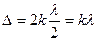(20.8)

(k = 0,1,2,3, … - порядок интерференционного максимума)

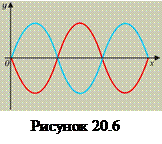Условие минимума: При наложении световых волн колебания ослабляют друг друга в тех точках пространства, куда волны приходят в противофазе, тогда амплитуда колебаний получается минимальной (рис. 20.6). Такое возможно при условии, что разность хода световых волн равна нечётному числу полуволн:

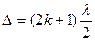(20.9)

(k = 0,1,2,3, … - порядок интерференционного минимума)

Ø Расчёт интерференционной картины от двух когерентных источников

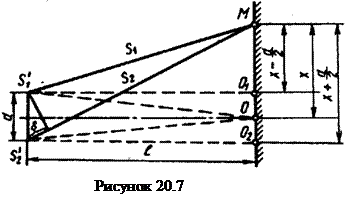
Рассмотрим два монохроматических когерентных источника S₁^' и S₂^', находящихся на расстоянии d друг от друга (рис.20.7). Расстояние от источников до экрана равно ℓ›› d. Bыберем на экране произвольную точку М, положение этой точки на экране определяется координатой х, отсчитываемой от точки, равноудалённой от когерентных источников S₁ и S₂. В точке О всегда наблюдается усиление света, так как разность хода интерферирующих волн равна нулю. По мере удаления от центра экрана (точки О) наблюдается чередование тёмных и светлых полос. Чтобы выяснить, что будет в точке М, определим разность хода Δ от источников S₁ и S₂ . Из рис.5 следует, что

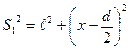
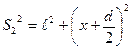
откуда

S₂² - S₁² =( S₂ + S₁) (S₂ - S₁) = 2xd

При вычислении были сделаны следующие допущения: так как

ℓ›› d, то S₁ + S₂ =2ℓ, а S₁ – S₂ = Δ. Тогда

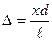(20.10)

Если для точки М 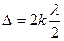, то в этой точке наблюдается усиление света. Следовательно, любая точка экрана, имеющая координату x_k и удовлетворяющая условию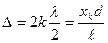

откуда

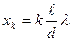(20.11)

где k = 0,1,2,…, будет иметь максимум интенсивности.

Если для точки М 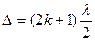, то в этой точке наблюдается гашение света.

Следовательно, любая точка экрана, имеющая координату x_k и удовлетворяющая условию

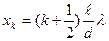(20.12)

где k = 0,1,2,…, будет иметь минимум интенсивности.

Зная координаты максимумов и минимумов, можно рассчитать ширину интерференционной полосы, т.е. расстояние между соседними минимумами:

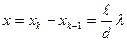(20.13)

Анализируя полученное выражение, можно сделать вывод, что ширина Δx интерференционной полосы увеличивается с уменьшением расстояния d между источниками. Для того, чтобы интерференционная картина чётко наблюдалась, необходимо соблюдение условия ℓ›› d. Если источник света монохроматический, то интерференционная картина будет представлять собой ряд чередующих светлых и тёмных полос. При белом источнике света полосы на экране будут цветными, за исключением центральной, где для лучей любой длины волны будет своя разность хода ∆. При этом красные лучи удалены от центральной полосы на большее расстояние, чем фиолетовые, вследствие того что λ_кр › λ_ф.