Кольца Ньютона

Особый исторический интерес представляет случай интерференции в тонком воздушном слое, известный под именем колец Ньютона. Эта картина наблюдается, когда выпуклая поверхность линзы малой кривизны соприкасается в некоторой точке с плоской поверхностью хорошо отполированной пластинки, так что остающаяся между ними воздушная прослойка постепенно утолщается от точки соприкосновения к краям. Если на систему (приблизительно нормально к поверхности пластинки) падает пучок монохроматического света, то световые волны, отраженные от верхней и нижней границ воздушной прослойки, будут интерферировать между собой. При этом получается следующая картина: в точке соприкосновения наблюдается черное пятно, окруженное рядом концентрических светлых и черных колец убывающей шириyы.

Нетрудно рассчитать размеры и положение колец Ньютона, предполагая, что свет падает нормально к поверхности пластинки, так что разность хода, обусловленная толщиной прослойки δ, равна 2δn, где п — показатель преломления вещества прослойки. В случае воздуха п можно считать равным единице. Толщина δ_m, соответствующая m -му кольцу, связана с радиусом этого кольца r_m и радиусом кривизны линзы R соотношением

δ_m = r_m²/2R

Принимая во внимание различия в условиях отражения от верхней и нижней поверхностей прослойки (потеря полуволны), найдем условие образования т-го темного кольца

Δ _m = 2 δ_m+ ½ λ = (2m + 1) ½ λ

или

δ_m= ½ λm

откуда

(5.1)

где т — целое число. В частности, m= 0 и r_m = 0 соответствуют темноте (объяснение центрального темного пятна). Чем больше m, тем меньше различие между радиусами соседних колец, (r_m+1 и r_m), т. е. тем ближе друг к другу кольца. Измерив r_m и зная т и R, можно из описанного опыта найти длину волны λ . Определения эти довольно точны и легко выполнимы.

Интерференционная картина будет отчетливой при малом δ (тонкая прослойка). Это не препятствует, однако, получению колец заметного радиуса, ибо 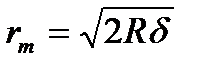, а R — радиус кривизны линзы — может быть взят значительным (обычно 100—200 см).

Если падающий свет — немонохроматический, то разным λ соответствуют разные r_m, т. е. вместо черных и светлых колец мы получим систему цветных колец. Полагая в формуле (5.1) т = 1, найдем область, занимаемую кольцами первого порядка, т = 2 — кольцами второго порядка и т. д. Нетрудно видеть, что фиолетовый (λ = 400 нм) максимум второго порядка совпадает с темно-красным (λ = 800 нм) максимумом первого порядка; на красный максимум второго порядка накладывается фиолетовый максимум четвертого порядка и зеленый (λ = 530 нм) максимум третьего порядка и т. д. Так как, кроме того, каждое кольцо имеет заметную ширину и в нем осуществляется плавный переход от максимума к минимуму, то даже в пределах первого порядка происходит значительное наложение одних цветов на другие; в еще большей степени это имеет место у высших порядков. В результате такого наложения возникает своеобразное чередование оттенков, совершенно не напоминающее последовательности «радужных цветов».