Модель розподілу ресурсів

Модель «затрати-випуск»В.В. Леонтьєва характеризує лише деякі особливості закритого виробництва. Насправді ситуація складніша, оскільки за умови закритого виробництва необхідні початкові ресурси для початку виробництва, які під час функціонування економічної системи можуть відтворюватися, але в стартовій ситуації мають бути в наявності як складова частина виробництва. Залежно від кількості цих ресурсів прибуток буде різним, а тому виникає задача раціонального (оптимального) їх розподілу.

Будемо вважати, що, крім балансових рівнянь В.В. Леонтьєва (3.1), (3.2) у нашій моделі є критерій оптимальності:

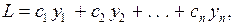
який характеризує сумарний прибуток об’єкта економічної діяльності. 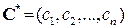– вектор вартостей; 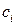– вартість одиниці продукції і-го виду .

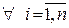Крім того, задано вектор 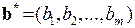, що характеризує запаси ресурсів, які є на виробництві. Задано матрицю 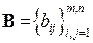з невід’ємними елементами, тоді можна записати

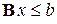
або

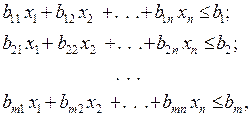
де 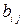– нормативний коефіцієнт, який характеризує кількість і-го ресурсу необхідного для виготовлення одиниці j-го продукту із застосуванням заданого технологічного циклу в виробництві.

Звідси випливає, що задачу розподілу ресурсів можна сформулювати так: потрібно знайти такий набір значень компонент вектора 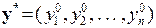для якого виконується умова (забезпечення максимального прибутку):

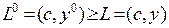
при

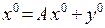
та

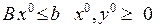(4.1)

Якщо матриця 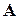продуктивна, то з (3.1) можна знайти 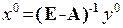, а підставивши х⁰ у (4.1) одержимо задачу: знайти 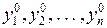такі, щоб

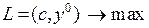,(4.2)

а

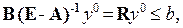(4.3)

де ,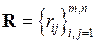

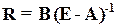
До виробничих (технологічних) обмежень можуть бути долучені і обмеження екологічного, соціального характеру та ін. Тому серед обмежень (4.2), (4.3) можуть бути і такі, що потребують виконання їх або нерівностей оберненого знака до (4.2), (4.3). У загальному вигляді задача оптимального розподілу ресурсів зводиться до розв’язання задачі лінійного програмування (ЗЛП).