Модель «затрати-випуск» В. В. Леонтьєва
Розглянемо найпростішу модель «затрати-випуск» – замкнену і статичну [3]. Будемо вважати, що об’єкт економічної діяльності випускає 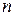 найменувань продукції
найменувань продукції 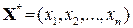 , де значок «*» при векторі
, де значок «*» при векторі 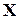 означає операцію транспонування. Крім того,
означає операцію транспонування. Крім того,

де Z – вектор внутрішнього споживання продукції об’єктом;
Y – вектор кінцевої продукції (продукції, яка йде на продаж, у запаси, тощо).
Будемо вважати, що
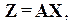
де 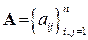 – невід’ємна матриця своїх елементів, які є коефіцієнтами прямих затрат при виробництві продукції. Або
– невід’ємна матриця своїх елементів, які є коефіцієнтами прямих затрат при виробництві продукції. Або
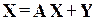 (3.1)
(3.1)
У деталізованому вигляді матричне рівняння (3.1) має вигляд:
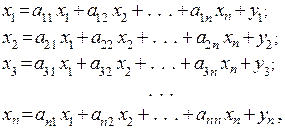 (3.2)
(3.2)
де 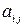 – кількість продукції і-го виду, потрібної для виробництва одиниці продукції j-го виду.
– кількість продукції і-го виду, потрібної для виробництва одиниці продукції j-го виду. 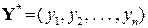 – компоненти вектора кінцевого випуску. Зміст компонентів вектора
– компоненти вектора кінцевого випуску. Зміст компонентів вектора 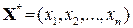 – кількість валового продукту відповідної номенклатури.
– кількість валового продукту відповідної номенклатури.
Будемо вважати, що технологічні коефіцієнти 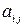 задано наперед. Модель (3.2) дозволяє за умов, коли, задано вектор Y, визначити розміри відповідних значень вектора валового продукту
задано наперед. Модель (3.2) дозволяє за умов, коли, задано вектор Y, визначити розміри відповідних значень вектора валового продукту 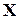 , виробничу собівартість випуску кожного виду продукції, матрицю повних затрат і дослідити на продуктивність матрицю А.
, виробничу собівартість випуску кожного виду продукції, матрицю повних затрат і дослідити на продуктивність матрицю А.
Матриця А називається продуктивною (інколи вживають термін цілком продуктивна), якщо матриця 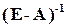 не має від’ємних елементів. Матриця
не має від’ємних елементів. Матриця
Е– одинична матриця розмірності (n×n).
Приклад.Нехай матриця А має вигляд
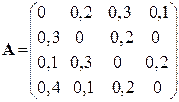
вектор  .
.
Знайти:
а) матрицю повних затрат  ;
;
б) вектор валового випуску 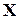 ;
;
в) виробничу собівартість S1, S2, S3, S4 кожного виду продукції.
Розв’язування. Шукаємо матрицю 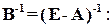
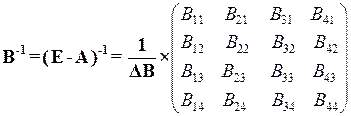

де 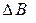 – детермінант (визначник) матриці
– детермінант (визначник) матриці 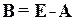 (det B =
(det B = 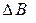 ):
):
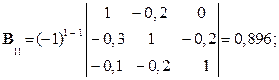
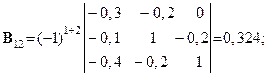
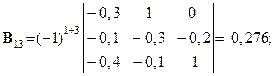
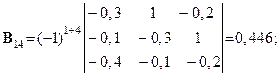
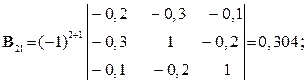
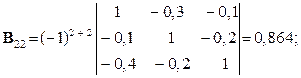

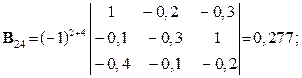
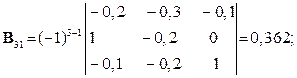


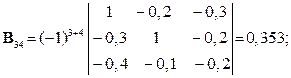
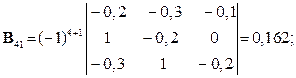
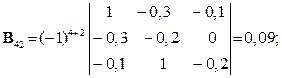
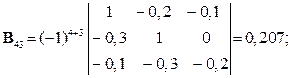
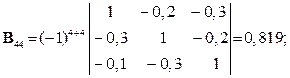
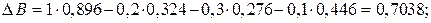
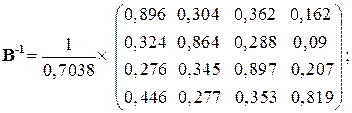
Шукаємо вектор валового випуску 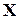 :
:
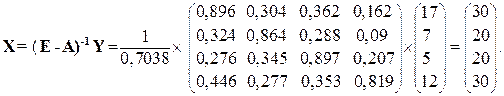
Шукаємо виробничу собівартість S1, S2, S3, S4 :
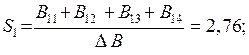

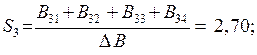
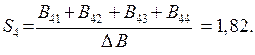
Часто виникає необхідність встановлення факту продуктивності матриці 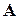 без знаходження елементів матриці
без знаходження елементів матриці 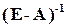 . Справедливі наступні твердження:
. Справедливі наступні твердження:
Твердження 1. Для продуктивності матриці 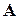 достатнє виконання умов:
достатнє виконання умов:
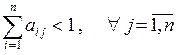 або
або 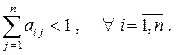
Твердження 2. Згідно з [5] для продуктивності матриці 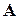 необхідне і достатнє виконання таких умов:
необхідне і достатнє виконання таких умов:
1) існує рядок і0 у матриці 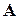 для якого виконується умова:
для якого виконується умова:
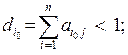
2) існує перенумерація рядків і стовпців матриці 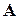 , для якої виконуються умови
, для якої виконуються умови
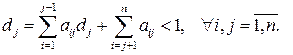
Припустімо, що  , тоді
, тоді 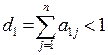 .
.
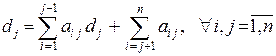 ,
,
де


...
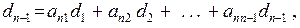
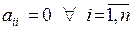
Звідси випливає, що продуктивність матриці 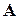 можна встановити за допомогою незначних обчислень і перенумерації компонент вектора
можна встановити за допомогою незначних обчислень і перенумерації компонент вектора 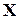 та елементів матриці
та елементів матриці 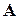 .
.
Завдання для самостійних і контрольних робіт
Знайти:
a) вектор валового випуску;
b) матрицю повних затрат;
c) виробничу собівартість кожного виду продукції;
| 1. | 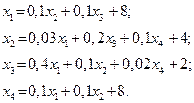
| 2. | 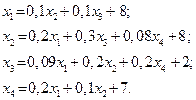
|
| 3. | 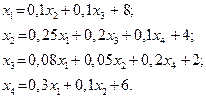
| 4. | 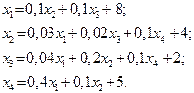
|
| 5. | 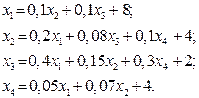
| 6. | 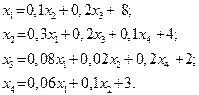
|
| 7. | 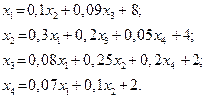
| 8. | 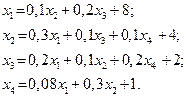
|
| 9. | 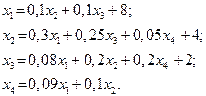
| 10. | 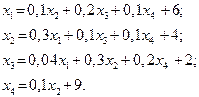
|
| 11. | 
| 12. | 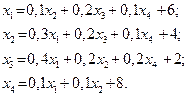
|
| 13. | 
| 14. | 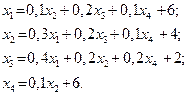
|
| 15. | 
| 16. | 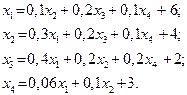
|
| 17. | 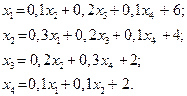
| 18. | 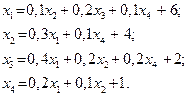
|
| 19. | 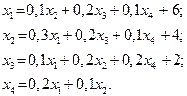
| 20. | 
|
| 21. | 
| 22. | 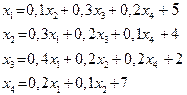
|
| 23. | 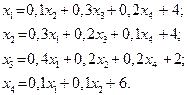
| 24. | 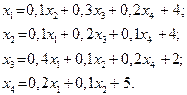
|
| 25. | 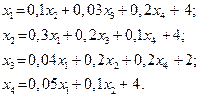
| 26. | 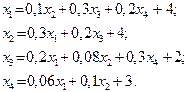
|
| 27. | 
| 28. | 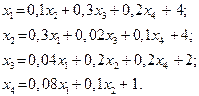
|
| 29. | 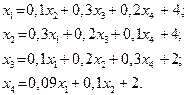
| 30. | 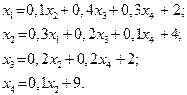
|
Дата добавления: 2015-06-12; просмотров: 1305;
