Методика роботи з книжкою на прикладі теми «Властивості логарифмів».

1. Прочитати параграф «Властивості логарифмів».

2. Відповісти на раніше поставлені до тексту завдання

3. Скласти план відповіді за прочитаним текстом.

9. Для чого потрібна актуалізація опорних знань і способів дій? Запропонуйте реалізацію цього етапу навчального процесу до теми «Розв’язування рівнянь і нерівностей з модулем».

Дуже важливим етапом на уроці математики є актуалізація опорних знань учнів перед введенням нових понять чи поясненням нового матеріалу . Логічно пов’язане між собою нове і старе сприяє системності наукового пізнання. Наступну тему учень може краще засвоїти лише тоді, якщо під час її вивчення нові уявлення і поняття асоціюються з уже набутими.

В педагогіці використовується словосполучення «актуалізація опорних знань», «актуалізація життєвого досвіду». Існує концепція проблемного навчання, згідно якої актуалізація - це розширення, поглиблення знань за допомогою раніше засвоєного і нове застосування попередніх знань.

Актуалізація опорних знань проводиться з метою:

- допомогти створенню у свідомості учнів системи навчального предмета, установленню взаємозв’язку між його частинами;

- сприяє закріпленню в пам’яті найважливіших фактів, правил, законів тощо, систематизуючи їх;

- забезпечує цілісне уявлення про досліджуваний матеріал;

- підготовляє учнів до усвідомленого сприйняття матеріалу;

- забезпечує ґрунтовне засвоєння нового матеріалу, встановлен­ню в ньому нових зв’язків і співвідношень.

- допомагає вчителю з’ясувати глибину засвоєння знань, з’ясувати прогалини й організувати роботу з їх усунення.

- сприяє формуванню в учнів почуття успішності, впевненості у власних силах, бажання удосконалювати знання.

Мета актуалізації – пробудити інтерес до теми, викликати зацікавленість, схвилю­вати, спровокувати учнів пригадати те, що вони знають; відтворити знання, вмін­ня, що потрібні для по­дальшої роботи на уроці.

В процесі актуалізації створюються умови для: визначення того, що вже відомо, та того що можна ще дізнатися; пов’язання знання з досвідом учня; «відкриття», самостійного здобування знань; підвищення ролі учнів на уроці .

Як наслідок, актуалізуючи систему знань і вмінь, учень має можливість на основі отриманих знань і вмінь та накопиченого досвіду їх використання розглядати їх у змінених та нових ситуаціях.

Учитель має організувати роботу на уроці так, щоб усім учням було цікаво вчитися., щоб матеріал був зрозумілий і доступний, щоб кожен учень розраховував на свої сили, свої знання і вміння ( які він пригадав, поновив в пам'яті ). Учні мають володіти певним мінімумом знань і умінь, працювати на уроці разом з учителем, а робота має бути посильна для них, оскільки кожній дитині властивий свій темп сприймання навчального матеріалу. На кожному уроці це впроваджується на етапі актуалізації знань, умінь і навичок. У цьому і полягає один із принципів особистісно орієнтованого навчання.

Щоб активізувати увагу дитини, зацікавити її, допомогти їй подолати прогалини в знаннях, а також активізувати її розумові здібності, заставити кожного мислити, включитися в спільну цікаву, захоплюючу роботу по здобуттю нових математичних знань, учитель повинен удосконалювати власні знання, вивчати досвід своїх колег, опановувати новітні педагогічні технології, створюючи свій власний досвід роботи.

Уміння цікаво організувати етап актуалізації — це одна з умов його ефективності.

Методи та прийоми проведення актуалізації опорних знань і способів дій обираємо в залежності від логіки процесу навчання, складності матеріалу, типу уроку. Це може бути бесіда, усне опитування, евристичні питання, письмова робота, короткий запис відповідей, заповнення таблиць, повторення матеріалу за підручником, використання науково-популярної і довідникової літератури, аналіз схем , таблиць, малюнків, використання методів «мозкового штурму» , математичні диктанти з самоперевіркою та корекцією, виконання усних вправ за готовими малюнками, завдання типу « знайди помилку», задачі, до яких потрібно поставити запитання і лише потім їх розв’язати та ін.

Актуалізація опорних знань учнів (теоретична частина)

Запитання

1. Що таке модуль числа?

2. Чому дорівнює модуль додатного числа? Від'ємного числа? Числа 0?

3. Чому дорівнює х, якщо |х|=5?

Математичний диктант

1. Модуль числа 81, -16 дорівнює ....

2. Записати усі числа, які мають модуль 15.

3. Знайти значення виразу |-8|+|-12|.

4. Обчислити значення виразу ||а |-15|, якщо а=2.

5. Розв'язати рівняння |х|=9.

Актуалізація опорних знань учнів (практична частина)

Біля дошки два учні виконують завдання, записані на картках. Інші учні виконують завдання від чарівника Модуля.

Картка 1

Обчислити значення виразу |x|:|y|, якщо

а) ;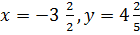

б) х=7,14, у=-0,07.

Картка 2

Позначити на координатній прямій числа, модулі яких дорівнюють 4; 7; 1,5; 0; 1.

Завдання

Учитель. Чарівник Модуль зашифрував цікавий вислів. Того, хто його розшифрує і правильно зрозуміє, чекає успіх у житті. А для цього потрібно обчислити:

1) |-7,2|-|3,4|; 2) |-1,2|∙|-6,4|;

3) |-12,1|-|-8,8|; 4) ;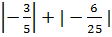

5) |-56|:|-0,7|; 6) |-0,81|:|0,9|.

Ключ

Відповідь. З НІЧОГО НІ ЧОГО НЕ БУВАЄ ( Тіт Лукрецій Кар – давньоримський поет і філософ).

10. За якою методичною схемою проходить процес формування понять? Опишіть процес формування поняття «Декартова система координат» в 6 класі.

Підготовча робо­та до введення координатної площини починається вже в 5 класі, де розглядають поняття «числовий промінь» і показують, як зобразити на ньому натуральні числа.

У 6 класі для зображення додатних і від'ємних чисел упрова­джується координатна пряма. Учні мають усвідомити, що положен­ня точки А на прямій цілком визначається одним числом, яке нази­вають координатою точки і позначають А (3), В(7, 8), М(х). Слід звернути увагу учнів, що одним числом визначають положення точки не лише на прямій. Наприклад, положення рухомого транспорту на залізниці чи автостраді можна визначити за номером кілометрового стовпа, який дорівнює відстані від певного пункту.

У 6 класі поняття про координати точки на прямій і на площині вводять описово на прикладах. Тут ще не ставлять за мету застосову­вати означення абсциси й ординати. Важливо, щоб учні усвідомили, що координата точки на прямій - це число, модуль якого дорівнює відстані точки прямої від початку відліку - точки О. Модулі першої та другої координат точки М на координатній площині задають від­стані цієї точки від осі х і осі у.

Уся система вправ на цьому етапі має бути спрямована на форму­вання вміння розв'язувати пряму й обернену задачі на визначення положення точки на координатній прямій і площині.

11. Наведіть класифікацію методів розв’язування рівнянь та їх конкретні приклади у темі «Квадратні рівняння».

1. Розв’язування квадратних рівнянь за формулою Х_1,2=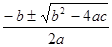

71x² –144x+ 73 = 0,

D= 144² — 4 · 71 · 73 = 4(72² — 71 · 73) = 4 (72² — (72²— 1)) = 4,

х_1,2= ,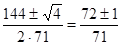

x₁ = 1, x₂ = .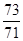

2.Графічне розв’язування квадратних рівнянь

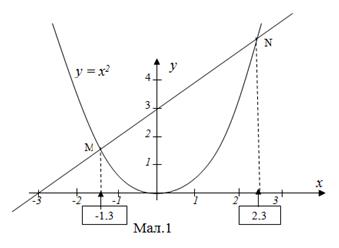
Розв'язати графічно рівняння x² - x - 3 = 0.

Розв'язання: x² = x + 3. Будуємо графіки функцій і y = x + 3.

Вони перетинаються в точках М і N, абсциси яких x₁≈-1,3 і x₂≈2,3.

3.Теорема Вієта

Якщо x₁ i x₂ – корені рівняння х² + рх + q=0, то х₁+ х₂ = -р, х₁ х₂= q.

х² - 6,5x + 9 = 0, дістали x₁ = 4,5; х₂ = 2. Перевірити, чи правильно розв'язано рівняння, можна так: 4,5 + 2 = -6,5; 4,5 · 2 = 9.

4.Розкладання на множники квадратного тричлена

Коли знаємо, що рівняння х² -5х + 6 = 0 має корені 2 і 3, то многочлен, що є в його лівій частині, можна розкласти на множники

х²-5х + 6 = (х - 2) (х - 3)

І навпаки, якщо ми знаємо розклад многочлена

х² + 3x - 4 = (x - 1)(x + 4),

то зразу можемо писати, що рівняння х² + 3х - 4 = 0 має такі корені: x₁ = 1, x₂ = - 4

12. Запропонуйте класифікацію задач у шкільному курсі геометрії. Опишіть методику розв’язування наступної задачі: «Доведіть, що площа ромба дорівнює половині добутку його діагоналей».

Оскільки, останнім часом здійснюються спроби дослідити задачі як такі, а не лише процес їх розв'язування, то звертається увага на потребу мати чітке уявлення про структуру задачі. Відомо, що кожна задача містить умову (умови) і вимогу (вимоги). Залежно від того, яку вимогу поставле­но в задачі, можна розрізнити задачі на:

Ø Обчислення;

Ø Доведения;

Ø Побудову;

Ø Дослідження.

У задачах на обчислення потрібно знайти число (або множину чи­сел) за даними числами і умовами, якими вони пов'язані між собою та з невідомими числами.). Наприклад,

Задача. Довжина одного із катетів прямокутного трикутника більше довжини другого на 10 см, але менше довжини гіпотенузи на 10 см. Знайдіть довжину гіпотенузи даного трикутника.

У задачах на доведення потрібно довести сформульоване в них твердження. Такою задачею, можна вважати і будь-яку теорему, чи властивість тої чи іншої фігури. Наприклад,

Задача. Доведіть, що середини сторін випуклого чотирикутника являються вершинами паралелограмма.

До задач на побудову належать як геометричні задачі, в яких потрібно побудувати певну фігуру, що задовольняє умову задачі, так і задачі на побудову графіків функцій, діаграм, перерізів багатогранників та інших тіл. Наприклад,

Задача. Через точку перетину двох даних кіл, провести пряму так, щоб кола відсікали на цій прямій рівні хорди.

У задачах на дослідження потрібно дослідити що-небудь. Наприклад:

Задача. Відрізки АВ і СD рівні. В якому випадку існує паралельне перенесення,