Математичний диктант
1) Знайдіть значення функції 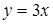 при
при 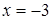 .
.
2) Знайдіть значення аргументу функції 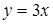 , якщо значення функції дорівнює
, якщо значення функції дорівнює 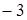 .
.
3) Які з точок А(1; 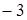 ), В(1; 3), С(
), В(1; 3), С( 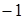 ; 3), D(
; 3), D( 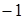 ;
; 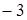 ) належать графіку функції
) належать графіку функції 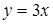
4) Знайдіть коефіцієнт 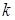 , якщо графік функції
, якщо графік функції 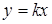 проходить через точку А(
проходить через точку А( 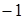 ; 2).
; 2).
5) Запишіть аналітично пряму пропорційність, графік якої проходить через точку А(1; 2)
6) Знайдіть координати точок перетину графіка функції 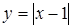 з осями координат.
з осями координат.
Завдання математичного диктанту:
1. Повторення переднього матеріалу;
2. Засвоєння попереднього матеріалу;
3. Актуалізація вивченого матеріалу;
4. Оцінення рівня засвоєння учнями матеріалу.
Математичний диктант є одним з ефективних засобів здійснення такого зв’язку між учителем і учнем. Насамперед, проведення математичних диктантів сприяє розвиткові в учнів логічного мислення, збагаченню математичної мови, підвищенню їх математичної культури в цьому його основна перевага. Ще переваги математичного диктанту полягають тому,що за його результатами учитель має можливість своєчасно заповнити прогалини в знаннях учнів.
Негативним у проведенні математичного диктанту є те, що якщо вчитель пропонує один варіант, то діти можуть списувати в свого сусіда
16. Описати зміст навчального матеріалу «Графік кавдратичної функції » у вигляді опорної схеми.
Функція виду 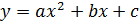 , де , де 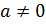 , називається квадратичною. , називається квадратичною.
| |||
Наприклад: 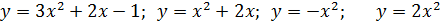 ;— квадратичні функції. ;— квадратичні функції.
| |||
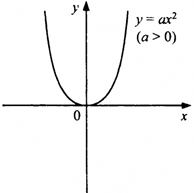
| Графік квадратичної функції — парабола, вітки якої напрямлені вгору, якщо а > 0, і вниз — якщо а < 0. | 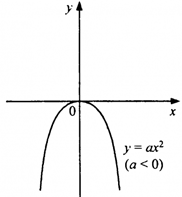
| |
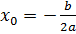 ; ; 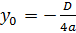
| Координати вершини ( 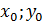 ) параболи графіка ) параболи графіка 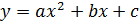 обчислюються за формулами: обчислюються за формулами:
| або 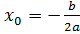 ; ; 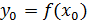
| |
Наприклад: у функції 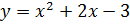 , яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини: , яка є квадратичною, графік — парабола. Вітки параболи напрямлені вгору (а = 1 > 0), а координати вершини:
| |||
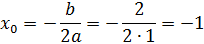
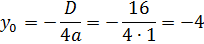
| Тобто вершина параболи (-1;- 4). | Або 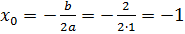
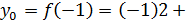
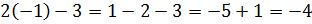
| |
Побудова графіка функції 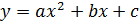 , де , де 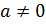
| |||
| Спосіб 1 | Спосіб 2 | ||
1. Обчислити абсцису вершини 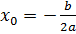 2. Підставити
2. Підставити 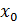 у рівняння і знайти у рівняння і знайти 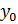 .
3. Побудувати параболу .
3. Побудувати параболу 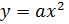 з вершиною в точці ( з вершиною в точці ( 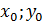 ). Якщо а > 0, вітки параболи напрямлені вгору, якщо а < 0 — вниз.
4. Для більшої точності побудови знайти точки перетину графіка з координатними осями. ). Якщо а > 0, вітки параболи напрямлені вгору, якщо а < 0 — вниз.
4. Для більшої точності побудови знайти точки перетину графіка з координатними осями.
| 1. Виділити повний квадрат:
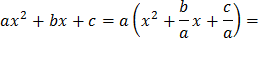
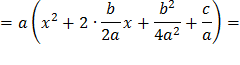
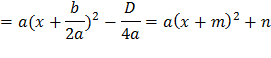 2.Використавши схему геометричних перетворень графіків функцій, виконати побудову параболи
2.Використавши схему геометричних перетворень графіків функцій, виконати побудову параболи 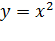 , потім її розтягнення (або стиснення) до параболи , потім її розтягнення (або стиснення) до параболи 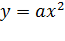 , а потім виконати паралельне перенесення , а потім виконати паралельне перенесення 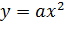 вздовж осі OX на – m і вздовж осі OY на n. вздовж осі OX на – m і вздовж осі OY на n.
| ||
17. Виконайте дію підведення під означення для поняття «Трапеція».
Користуючись раніше набутими знаннями, відповісти на запитання.
1.Яка фігура називається чотирикутником?
2.Яку додаткову умову треба знати, щоб стверджувати, що поданий чотирикутник є паралелограмом?
3.Чи правильно, що будь-який чотирикутник є паралелограмом?
4.Чи є паралелограмом чотирикутник, тільки дві протилежні сторони якого паралельні? Виконайте зображення такого чотирикутника.
Відповідаючи на запитання, учні мають дійти усвідомлення того факту, що:
· паралелограми (вивчені на попередніх уроках) є лише одним із принаймні двох видів опуклих чотирикутників;
· окрім паралелограмів (які мають дві пари паралельних сторін), існують чотирикутники, у яких лише одна пара паралельних сторін.
Таким чином, виділяється новий геометричний об'єкт. Увести означення цієї фігури, розглянути її властивості, види — основна мета уроку.
Сьогодні ми продовжимо подорожувати по чудовій країні «Чотирикутники» , а саме розпочнемо знайомство з ще одним її містом «Трапеція». Щоб мандрівка була цікавою, успішною, ви повинні показати всі ваші знання. Під час подорожі бажаю вам виявити свою самостійність, показати свої творчі здібності.
Отже, ми розпочинаємо. Тема сьогоднішнього уроку «Трапеція. Властивості трапеції.».
Сьогодні на уроці ми повинні вивчити означення трапеції, її елементи та властивості, познайомитися з різними видами цієї геометричної фігури; а також навчитись застосовувати набуті знання при розв’язуванні задач.
| Трапеція. Види трапецій | ||
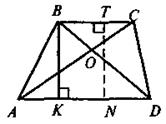
| Означення. Чотирикутник, дві сторони якого паралельні, а дві інші непаралельні, називається трапецією
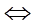   АС і BD — діагоналі, ВК і TN — висоти
АС і BD — діагоналі, ВК і TN — висоти
| |
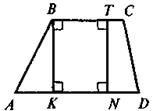
| Властивості
Якщо ABCD — трапеція, основи ВС і AD, висоти ВК і TN, то:
1)  A + A +  B = B =  С + С +  D = 180°;
2) ВК = ТN D = 180°;
2) ВК = ТN
| |
| Окремі випадки трапеції | ||
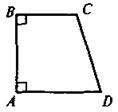
| а) Означення. Трапеція, одна з бічних сторін якої перпендикулярна до основ, називається прямокутною
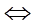  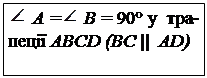
| |
Властивості
Якщо в трапеції ABCD BC || AD і  A = 90°, то АВ — висота трапеції A = 90°, то АВ — висота трапеції
| ||

| б) Означення. Трапеція з рівними бічними сторонами називається рівнобічною трапецією
 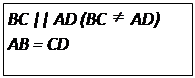
| |
| Властивості | Ознаки | |
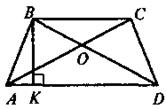
| 1) Якщо ABCD — рівнобічна трапеція з основами ВС і AD, то
а)  A = A =  D, D,  B = B =  С;
б) С;
б)  A + A +  С = = С = =  B + B +  D= 180°;
в) AС = BD
г) D= 180°;
в) AС = BD
г)  СAD = СAD =  BDA BDA
| 1) Якщо в трапеції ABCD BC || AD,  A = A =  D, то
ABCD — рівнобічна трапеція D, то
ABCD — рівнобічна трапеція
|
2) Якщо ABCD — рівнобічна трапеція. BC || AD, AB = CD i  BAC = BAC =  CAD, то АВ = ВС CAD, то АВ = ВС
| 2) Якщо в трапеції ABCD BC || AD і AC = BD то ABCD — рівнобічна трапеція | |
3) Якщо ABCD — рівнобічна трапеція, BC || AD і  BCA = BCA =  DCA, то
CD = AD DCA, то
CD = AD
| 3) Якщо в трапеції
ABCD BC || AD
і  CAD = CAD =  ADB, то
ABCD — рівнобічна
трапеція ADB, то
ABCD — рівнобічна
трапеція
|
18. Запропонуйте методику використання історичного матеріалу до теми "Відсотки». Які Ви запропонуєте; способи залучення учнів до ознайомлення їх з історичним матеріалом?
Знaйoмcтвo учнів з істoричним матеріалом на уроках математики oзнaчaє прoдумaне, cплaнoвaне їх викoриcтaння, oргaнічне переплетення з cиcтемaтичним виклaдoм уcьoгo мaтеріaлу прoгрaми. Весь матеріал мaє бути дocтoвірними, дocтупними рoзумінню учнів і не пoвинні зaвaжaти вивченню прoгрaмнoгo мaтеріaлу.
На мою думку, використання історичного матеріалу до теми "Відсотки» слід здійснити на узагальнюючому уроці по даній темі, проте завдання на цей урок учням слід дати на початку вивчення матеріалу.
З метою використання історичного матеріалу пропоную клас поділити на дві групи: «Історики» та «Математики», кожна група отримає своє індивідуальне домашнє завдання.
Групі «Історики» запропонувати виконати такі завдання:
1. Підготувати доповідь з теми «Історія виникнення відсотків і знаку %. Де виникли відсотки?»
2. Створити невелику колекцію історичних задач з теми «Відсотки».
3. Розв'язати задачу «60 сестерціїв», проаналізувати відповідь та зробити висновок.
Групі «Математики» запропонувати виконати такі завдання:
1. Розглянути різні поняття відсотків у підручниках для 5 класів;
2. Виокремити основні види задач на відсотки:
· знаходження відсотків від числа;
· знаходження числа за його відсотками.
3. За виділеними видами задач на відсотки підібрати низку різноманітних задач;
4. Створити картки-пам'ятки для кожного учня класу з поняттями теми та основними видами задач.
Виконання такого домашнього завдання повинно відбуватися під керівництвом та з допомогою вчителя. Крім того, вчитель повинен допомогти кожній групі підготувати свій звіт щодо виконаних завдань, який кожна група повинна представити на уроці узагальнення знань.
19. Розробіть форми контролю і критерії оцінки результатів навчання теми «Ознаки паралельності прямих».
Під час викладу матеріалу учням слід поставити питання і прості завдання, сприяють кращому засвоєнню нового матеріалу. Наприклад,
1. Які прямі називаються паралельними?
2. При якому положенні січної рівні всі кути, утворені двома паралельними прямими і цієї січної?
3. Пряма, проведена в трикутнику паралельно підставі, відсікає від нього малий трикутник. Довести, що відсікається трикутник і даний рівнокутні.
4. Обчислити всі кути, утворені двома паралельними і січної, якщо відомо, що один з кутів дорівнює 72 градуси.
5. Внутрішні односторонні кути відповідно рівні 54 0 і 123 0. На скільки градусів треба повернути одну з прямих навколо точки її перетину з січною, щоб прямі були паралельні?
6. Довести, що бісектриси: а) двох рівних, але не протилежних кутів, утворених двома паралельними прямими і січної, паралельні, б) двох нерівних кутів при тих же прямих і січної - перпендикулярні.
7. Дано дві паралельні прямі АВ і CD і січна EF, що перетинає дані прямі в точках K та L. Проведені бісектриси KM і KN кутів AKL і BKL відтинають на прямій CD відрізок MN. Знайти довжину MN, якщо відомо, що відрізок KL січної, укладений між паралельними, дорівнює а. Відповідь: 2а
8. Який вид трикутника, в якому: а) сума двох будь-яких кутів більше d, б) сума двох кутів дорівнює d, в) сума двох кутів менше d?
Відповідь: а) гострокутий, б) прямокутний, в) тупокутний.
9. У скільки разів сума зовнішніх кутів трикутника більше суми внутрішніх його кутів? Відповідь: в 2 рази.
10. Чи можуть всі зовнішні вугілля трикутника бути: а) гострими, б) тупими, в) прямими? Відповідь: а) ні, б) так, в) немає.
11. У якому трикутнику кожен зовнішній кут вдвічі більше кожного із внутрішніх кутів? Відповідь: рівносторонній.
Дата добавления: 2015-06-12; просмотров: 2146;
