Задача. Скільки потрібно фарби, щоб пофарбувати кулю діаметром 2,4 м, якщо на пофарбування 1 м2 витрачається 120 г фарби?
Довести, що площа ромба дорівнює половині добутку його діагоналей.
Перед розв’язанням такої задачі, необхідна актуалізація опорних знань, а саме: повторити:
1. Площа прямокутного трикутника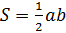 
;
2. Властивості діагоналей ромба:
Ø в точці перетину діагоналі ромба діляться пополам,
Ø діагоналі ромба ділять кути ромба пополам;
Ø діагоналі ромба, ділять його на 4 рівних прямокутних т-ки (котрі рівні за катетами).
Саме доведення, проводиться в такому форматі:
Нехай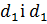 
– діагоналі ромба. Вони поділили ромб на 4 рівних прямокутних т-ки з катетами: 
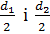. Тоді площа ромба 
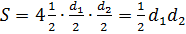, що і треба було довести.
13. Які функції має виконувати наочність? Запропонуйте методику використання наочності у темі «Нерівності».
Сутність наочності можна передати висловом: «краще один раз побачити, ніж сто раз почути». Вона вважається похідним принципом від принципу доступності: чим насиченішим є унаочнене заняття, тим доступнішим буде пояснення нової теми.
Наочність виконує такі функції:
- сприяє розумовому розвитку суб’єктів учіння;
- допомагає виявити взаємозв’язки між науковими знаннями і життєдіяльністю, теорією і практикою;
- полегшує навчально-пізнавальну діяльність учнів і сприяє формуванню в них інтересу до професійних знань;
- допомагає сприймати предмет, що вивчається у його розмаїтті;
- сприяє формуванню мотивації пізнання довколишньої діяльності, тощо.
Методика використання наочності у темі «Нерівності»:
Вивчаючи тему «Нерівності», на початку першого уроку слід повторити з учнями означення додатних та від`ємних чисел та розв’язати вправи, подані на Кодоплівці 1.
| Використовуючи знак >або <, запишіть висловлення: а) -√2 – від’ємне число, б) 400 – додатне число, в) х – додатне число г) у – від’ємне число, д) –а – додатне число, е) –б – від’ємне число. Кодоплівка 1 |
Далі вчитель демонструє Таблицю 1, в якій заповнена лише ліва колонка. Пропонує учням записати її в зошит, надавши конкретних значень а і б, переконатися у вірності даних властивостей, сформулювати їх словами і записати у правій частині таблиці.
Таблиця 1
| Властивості нерівностей | |
| Символічний запис | Словесний запис |
| Якщо а >0, б> 0, то а+б >0, аб >0, а/б >0. | Сума, добуток і частка двох додатних чисел – додатні числа |
| Якщо а <0, б< 0, то а+б<0, аб >0, а/б >0. | Сума від’ємних чисел – число від’ємне, а добуток і частка двох від’ємних чисел – число додатне. |
| Якщо а >0, б <0, то аб< 0, а/б <0. | Добуток і частка додатного і від’ємного чисел – від’ємне числа. |
| Якщо аб >0(а/б >0), то або а >0 і б >0, або а< 0, б< 0. | Якщо добуток і частка двох чисел – додатне число, то ці числа мають однакові знаки. |
| Якщо аб< 0(а/б< 0), то або а >0 і б< 0, або а <0, б >0. | Якщо добуток і частка двох чисел – від’ємне число, то ці числа мають різні знаки. |
| Якщо аб <0, то а(2n) >0, а(2n+1)< 0. | Парний степінь від’ємного числа – число додатне, а непарний степінь від’ємного числа -- число від’ємне. |
Така робота дасть можливість засвоїти властивості, які будуть використовуватися при вивчені наступного матеріалу.
Для закріплення понять «більше», «менше» корисно запропонувати учням Таблицю 2.
Таблиця 2
| Дійсні числа та співвідношення між ними | |||
| |||
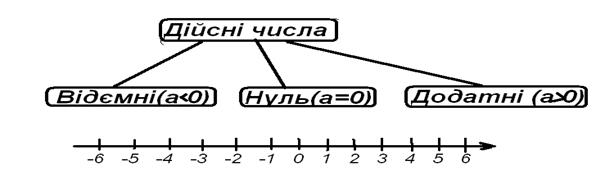
| Співвідношення | Запис | Означає | Графічне зображення |
| >(більше) | а >б | а-б >0 | 
|
| <(менше) | а <б | а-б <0 | 
|
| =( дорівнює) | а=б | а-б =0 | 
|
Розглядаючи нерівності і їх види, варто продемонструвати учням Кодоплівку 2, зміст якої учні мають занести в зошити.
Кодоплівка 2
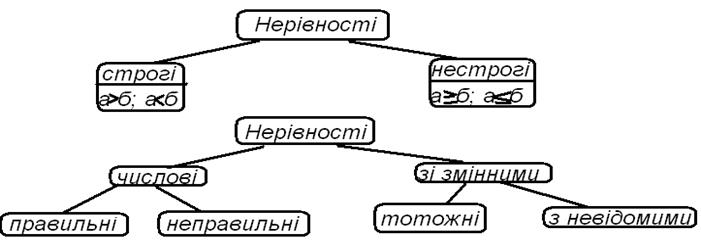
Так само за допомогою таблиць і кодоплівок можна провести не тільки пояснення матеріалу, а й інші етапи уроки.
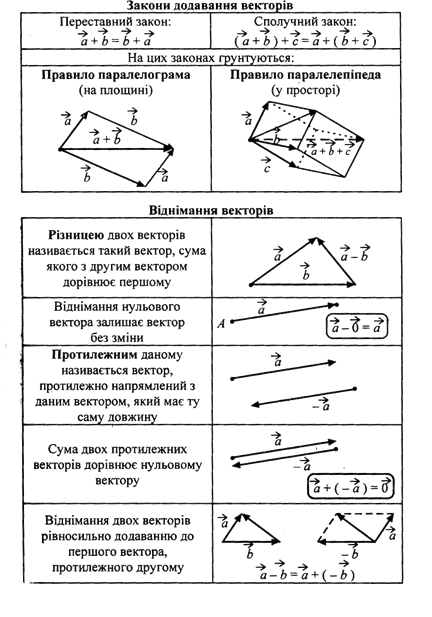
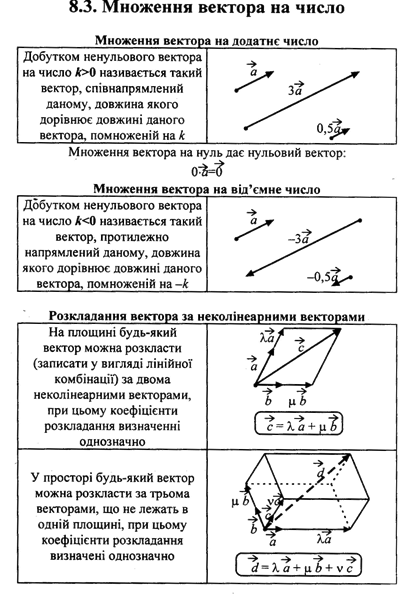
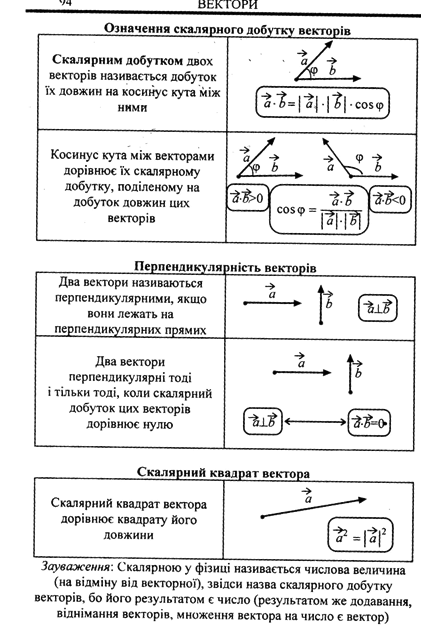
14. Розробити таблицю основних фактів теми «Вектори на площині», яку доцільно подати в узагальненому виді (варіант опорного конспекту)
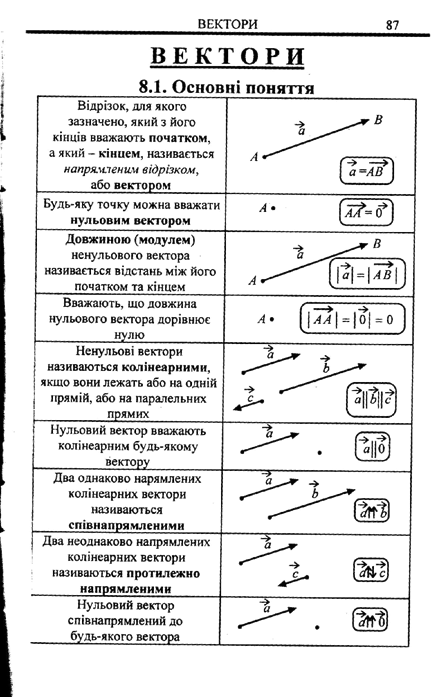
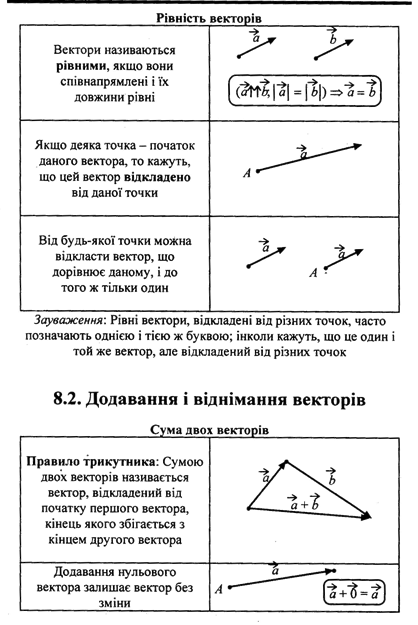
15. Запропонуйте математичний диктант до теми «Лінійна функція». Вкажіть завдання, позитивні та негативні сторони такого методу навчання.
Дата добавления: 2015-06-12; просмотров: 1722;