Яка перевага графічного способу розв'язування квадратних нерівностей перед аналітичним способом? Поясніть на конкретному прикладі.
Рішення рівнянь графічним способом дозволяє знайти точне або наближене значення коренів, дозволяє знайти кількість коренів рівняння.
При побудові графіків і рішення рівнянь використовуються властивості функції, тому метод частіше називають функціонально-графічним.
Для вирішення рівняння «ділимо» на дві частини, вводимо дві функції, будуємо їх графіки, знаходимо координати точок перетину графіків. Абсциси цих точок і є корені рівняння.
Аналітичний метод полягає у розчленуванні задачі на кілька простіших задач. Розв'язування починають з шуканої величини. У результаті аналізу відшукують закономірність, що зв'язує шукану величину з заданими. Якщо в закономірність входять крім шуканої величини інші невідомі, то шукають інші закономірності, що зв'язують їх з відомими в умові задачі. Розрахункова формула одержується як синтез окремих закономірностей.
Графічні способи вирішення рівнянь красиві і зрозумілі, але не дають стовідсоткової гарантії вирішення будь-якого рівняння. Абсциси точок перетину графіків можуть бути наближеними.
Дану нерівність можна розв’язати аналітичним та графічним способами.
Аналітичний :
1/x>x
1/x–x> 0
(1 –x2 )/x >0
x≠0
1 –x2>0
(1 –x)(1+x) >0
x = ±1;
Розв’язавши дану нерівність методом інтервалів одержимо її розв’язок

+ – + –

-1 0 1
xє (–∞;–1)V(0; 1)
Графічний :
 Побудуємо графіки функцій y=1/x, y=x та виберемоті проміжки осі абсцис, на яких графік функції y=1/xрозташований вище графіка функціїy=x.
Побудуємо графіки функцій y=1/x, y=x та виберемоті проміжки осі абсцис, на яких графік функції y=1/xрозташований вище графіка функціїy=x.
xє (–∞;–1)V(0; 1)
На мою думку у даномувипадкукращим є графічний спосіб, оскільки функції є нескладними і їх легко можна зообразити на координатній сітці, також учні наочно бачать розв’язок, що краще сприймається та засвоюється.
21. Запропонуйте мотивацію навчання теми «Ознаки подільності».
Мотивація вивчення теми «Ознаки подільності».
Звертаючись до касира магазина, покупець сказав:
– Візьміть, будь ласка, з мене за 2 пачки солі по 90 коп., за 2 куски мила по 2 грн. 70 коп., за 3 пачки цукру і за 6 коробочок сірників, але вартості пачки цукру і сірників не пам’ятаю.
Касир видав покупцеві чек на 29 грн. 17 коп. Подивившись на чек, покупець повернув його касирові і сказав:
– Підраховуючи загальну суму, Ви, безперечно, помилились.
Касир перевірив і погодився. Довелось вибачитись і видати покупцеві другий чек. Як покупець знайшов помилку?
Як це зробити? Сьогодні ви вивчите ознаки подільності.
22. Виконайте логіко-математичний аналіз навчального матеріалу теми «Розв'язування систем рівнянь другого степеню з однією змінною».
Для того щоб правильно організовувати роботу учнів по оволодінню алгоритмами шкільного курсу математики, учителю необхідно опанувати уміння виконувати логіко-математичний аналіз алгоритмів (правил).
Логічний аналіз алгоритмів (правил) припускає:
а) перевірку наявності у даного правила характеристичних властивостей алгоритму;
б) виділення послідовності операцій і логічних умов у даному правилі;
в) установлення зв'язку алгоритму (правила) з іншими знаннями.
Математичний аналіз алгоритмів (правил) складається зі встановлення математичної основи даного правила, тобто тих базових математичних положень, що дозволяють побудувати саме таке правило (вони звичайно називаються знаннями, що обґрунтовують).
Покажемо логіко-математичний аналіз правила на прикладі правила додавання десяткових дробів.
Приклад 1. Наведемо формулювання правила, що вивчається в V класі:
Щоб скласти два десяткових дроби, треба:
1) зрівняти число знаків після коми в доданках;
2) записати доданки один під одним так, щоб кома виявилася під комою;
3) додати отримані числа, як складають натуральні числа;
4) поставити в отриманій сумі кому під комами в доданках.
Насамперед звернемо увагу на виконання характеристичних властивостей алгоритму. У словесному формулюванні правила виділені дискретні кроки, кожний з який являє собою операцію, раніше сформовану в учнів (наприклад, додавання натуральних чисел, приписування нулів у дробовій частині десяткового дробу), і в цьому змісті елементарну чи дійсно найпростішу операцію (підписування доданків один під одним, постановка коми в результаті). Тому наведене правило має властивості дискретності й елементарності кроків.
У словесному формулюванні також строго зазначена послідовність кроків (усі кроки пронумеровані). Це говорить про те, що дане правило має властивість детермінованості.
Це правило має властивість масовості. Застосовуючи його, можна скласти будь-які два десяткові дроби. Потрібно тільки мати на увазі, що перша операція, виділена в правилі, виконується тільки тоді, коли число знаків у дробових частинах доданків різне.
Нарешті, застосовуючи дане правило, завжди знайдемо суму будь-яких двох десяткових дробів. Це означає, що дане правило має властивість результативності.
Таким чином, це правило додавання двох десяткових дробів володіє всіма характеристичними властивостями алгоритму, тому його можна назвати алгоритмом.
В алгоритмі вже виділені операції і зазначена їх послідовність. Однак, з огляду на зауваження, зроблене при розгляді властивості масовості, доцільно виділити логічну умову, що визначає число знаків у дробових частинах доданків.
Для того щоб виконати математичний аналіз алгоритму, необхідно за операціями алгоритму побачити їх математичну основу, чи, іншими словами, відповісти на запитання, на підставі яких математичних знань можна виконувати ту чи іншу операцію, що входить в алгоритм.
Операції алгоритму додавання двох десяткових дробів формалізують порозрядний принцип додавання цих чисел. Використання цього принципу (як і у випадку натуральних чисел) пов'язано з особливостями нумерації десяткових дробів (позиційний принцип запису десяткових дробів) і з можливістю застосування законів додавання для додавання одиниць одного розряду.
Приклад 2. При додаванні чисел 2,35 і 0,21 можна представити кожний з доданків у виді суми розрядних доданків:
2,35=2 + 0,3 + 0,05;
0,21=0,2+0,01.
Потім, застосувавши переставний і сполучний закони додавання, додати одиниці одного розряду, тобто:
(2 + 0,3 + 0,05) + (0,2 + 0,01)=2 + (0,3 + 0,2)+(0,05 + 0,01)+0,5+0,06=
=2 +0,5 + 0,06.
І нарешті, результат, записаний у вигляді суми розрядних доданків, представити у вигляді десяткового дробу 2,56.
Таким чином, що ґрунтовними знаннями для розглянутого алгоритму є правила нумерації десяткових дробів і закони додавання, що дають можливість виконувати додавання порозрядно.
Логіко-математичний аналіз алгоритму дозволяє правильно здійснити добір матеріалу для роботи з учнями по оволодінню алгоритмом.
Робота з учнями по оволодінню алгоритмом звичайно включає три основних етапи: 1) введення алгоритму; 2) засвоєння алгоритму; 3) застосування алгоритму.
Охарактеризуємо мету кожного з виділених етапів:
· мета першого етапу – актуалізація знань, необхідних для введення й обґрунтування алгоритму, а також формулювання алгоритму;
· мета другого етапу – відпрацьовування операцій, що входять в алгоритм, і засвоєння їхньої послідовності;
· мета третього етапу – відпрацьовування алгоритму в знайомих (при варіюванні вихідних даних) і незнайомих ситуаціях.
Основним засобом, що використовується на різних етапах формування алгоритму, є система вправ. Зміст її визначається на основі логіко-математичного аналізу конкретного алгоритму.
Можна виділити і домінуючі форми роботи з учнями на різних етапах формування алгоритму. Так, на першому етапі це усна робота на повторення. На другому етапі – письмова колективна робота з широким використанням коментування виконуваних дій. На третьому етапі – самостійна робота.
Алгоритми і правила мають спільне функціональне призначення – формування загальних методів розв'язання класу однотипних задач. Однак їх методичне призначення може бути різним. Алгоритм доцільно використовувати на перших етапах формування дії, так як він дає докладний опис послідовності операцій. Правило зручно застосовувати тоді, коли в основному вміння виконувати дію вже сформоване й учню не потрібно докладного опису операцій.
У шкільних підручниках, математики більшість правил сформульована в лаконічній і "стислій" формі. Для навчання учнів виконанню відповідного правила дії вчителю часто необхідно записати його у виді алгоритму.
Приклад 3. Покажемо, як це можна зробити, на прикладі правила множення двох десяткових дробів. У підручнику є додаткове зауваження про те, що іноді в добутку може вийти менше цифр, ніж необхідно відокремити комою, у цьому випадку ліворуч до добутку приписують нулі. З огляду на це зауваження, сформулюємо в словесній формі алгоритм множення двох десяткових дробів.
Щоб помножити один десятковий дріб на інший, треба:
1. підписати їх один під одним так, як при множенні натуральних чисел (не звертаючи уваги на коми);
2. виконати множення чисел як натуральних, не звертаючи уваги на коми;
3. підрахувати загальне число цифр після коми в обох множниках разом;
4. порівняти це число з числом цифр, отриманих у добутку;
5. якщо число цифр у добутку більше числа цифр, що стоять після коми в обох множниках разом, то у добутку праворуч відокремити стільки цифр комою, скільки їх після коми в обох множниках разом; якщо ні, то приписати до добутку ліворуч один чи декілька нулів і відокремити стільки цифр у добутку праворуч, скільки їх після коми в обох множниках разом.
23. Вивчення тем "Арифметична прогресія" і "Геометрична прогресія" дозволяють використовувати метод аналогії. Побудуйте для цього порівняльну таблицю основного теоретичного матеріалу.
| Арифметична прогресія | Означення | Геометрична прогресія |
Арифметичною прогресією називають послідовність  кожен член якої, починаючи з другого, дорівнює попередньому, до якого додається одне й те саме число d, яке називають різницею арифметичної прогресії кожен член якої, починаючи з другого, дорівнює попередньому, до якого додається одне й те саме число d, яке називають різницею арифметичної прогресії
| Геометричною прогресієюназивають послідовність  , кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число q (q≠0, |q|≠1), яке називають знаменником геометричної прогресії , кожний член якої, починаючи з другого, дорівнює попередньому, помноженому на одне й те саме число q (q≠0, |q|≠1), яке називають знаменником геометричної прогресії
| |
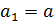 , , 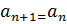 +d +d
| Рекурентна формула | 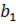 =b, =b, 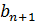 = = 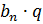
|
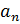 = = 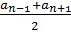
| Характеристична властивість | 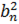 = = 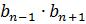
|
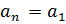 +d(n-1) +d(n-1)
| Формула n - ого члена | 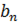 = = 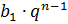
|
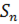 = = 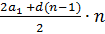 , ,
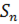 = = 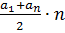
| Формула суми n перших членів | 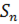 = = 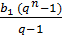
|
| Формула суми всіх членів геометричної прогресії (|q| <1) | S = 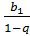
|
Дата добавления: 2015-06-12; просмотров: 2749;
