Закон Джоуля-Ленца в дифференциальной (локальной) форме

В проводнике переменного сечения в различных местах выделяется различная тепловая мощность. Найдем удельную тепловую мощность – мощность, выделяющуюся в единице объема проводника: .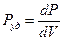

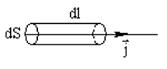Выделим элементарный объем в виде цилиндра, расположенного вдоль линии тока, с площадью оснований dS и длиной dl. Его сопротивление равно 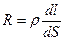. В этом объеме выделяется тепловая мощность 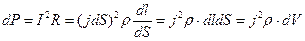. Удельная тепловая мощность, следовательно, равна:

.

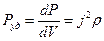2. Участок цепи с электродвигателем.

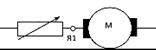Потребляя электроэнергию, электродвигатель развивает механическую мощность 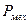. На участке цепи с электродвигателем необходимо различать мощность электрических сил и тепловую мощность тока.

Мощность электрических сил 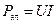– это полная мощность на участке цепи. Она идет и на выделение теплоты, и на совершение механической работы. Тепловая мощность при этом равна 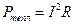, а закон сохранения энергии для этого участка цепи принимает вид:

.

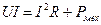Как видно из этого уравнения, сила тока в данном случае меньше, чем U/R.

Пример с электродвигателем показывает, что наиболее общее выражение для тепловой мощности тока, применимое во всех случаях (при наличии в цепи других, нетепловых, действий тока) – это:

, .

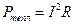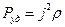Итак, закон Джоуля-Ленца можно сформулировать так:

Тепловая мощность тока 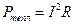; удельная тепловая мощность тока .

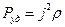Выражение 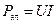определяет мощность электрических сил, которая не всегда совпадает с тепловой мощностью тока.

3. Неоднородный участок цепи.

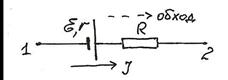Будем считать, что на участке есть источник тока, но не совершается механическая работа и нет химических превращений. Тогда сумма мощностей электрических и сторонних сил равна выделяемой на участке тепловой мощности:

.

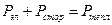Выберем направление обхода участка по току. Мощность электрических сил 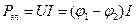(она может быть положительной или отрицательной, в зависимости от значений потенциалов точек 1 и 2).

Мощность сторонних сил 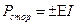(«плюс» – если источник включен по току, как на рисунке). Тепловая мощность 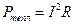. Таким образом:

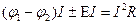, или .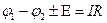

Исходя из соображений о сохранении энергии на участке цепи, мы пришли к закону Ома для неоднородного участка цепи.

Демонстрация. Тепловая мощность тока, выделяемая в лампе накаливания, в конечном итоге превращается в излучение (видимого и инфракрасного диапазонов).

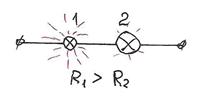На лампе указывают напряжение, на которое она рассчитана, и расчетную мощность. Обычно лампы подключаются к сети параллельно. Но на нашей схеме две разные лампы («100 Вт, 220 В» и «150 Вт, 220 В») включены последовательно. Какая из них горит ярче?

Ответ: 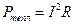, поэтому при одинаковой силе тока ярче горит лампа с бóльшим сопротивлением. Сопротивление лампы можно рассчитать по номинальным значениям Р и U: 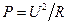, откуда 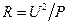. У лампы «100 Вт» сопротивление больше, поэтому в этой схеме она горит ярче, чем лампа «150 Вт».