Полная, полезная мощности и КПД цепи постоянного тока

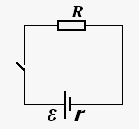
Рассмотрим замкнутую неразветвленную цепь, состоящую из источника тока и резистора.

Применим закон сохранения энергии ко всей цепи:

.

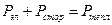Так как 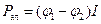, а для замкнутой цепи точки 1 и 2 совпадают, мощность электрических сил в замкнутой цепи равна нулю. Это равносильно утверждению о потенциальности электрического поля постоянного тока, о которой уже упоминалось ранее.

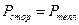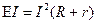Итак, в замкнутой цепи всё тепло выделяется за счет работы сторонних сил: , или , и мы снова приходим к закону Ома, теперь для замкнутой цепи: .

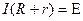Полной мощностью цепи называют мощность сторонних сил, она же равна полной тепловой мощности:

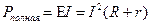(1).

Полезнойназывают тепловую мощность, выделяемую во внешней цепи (независимо от того, полезна она или вредна в данном конкретном случае):

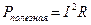(2).

КПД цепи

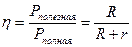(3).

Роль электрических сил в цепи. Во внешней цепи, на нагрузке R, электрические силы совершают положительную работу, а при перемещении заряда внутри источника тока – такую же по величине отрицательную. Во внешней цепи теплота выделяется за счет работы электрического поля. Работу, отданную во внешней цепи, электрическое поле «возвращает» себе внутри источника тока. В итоге вся теплота в цепи «оплачена» работой сторонних сил: источник тока постепенно теряет запасенную в нем химическую (или какую-то другую) энергию. Электрическое же поле играет роль «курьера», доставляющего энергию во внешнюю цепь.

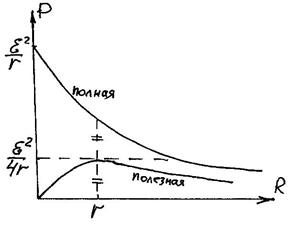Зависимость полной, полезной мощностей и КПД от сопротивления нагрузки R.

Эти зависимости получаем из формул (1 – 2) и закона Ома для полной цепи:

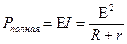. (4)

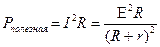. (5)

Графики этих зависимостей вы видите на рисунке.

Полная мощность монотонно убывает с ростом 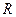, т.к. убывает сила тока в цепи. Максимальная полная мощностьвыделяется при 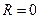, т.е. при коротком замыкании. Источник тока совершает максимальную работу за единицу времени, но вся она идет на нагревание самого источника. Максимальная полная мощность равна

.

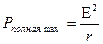Полезная мощность имеет максимум при 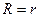(в чем вы можете убедиться, взяв производную от функции (5) и приравняв ее нулю). Подставив в выражение (5 ) 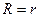, найдем максимальную полезную мощность:

.

Легко убедиться, что при 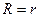полная мощность вдвое больше полезной.

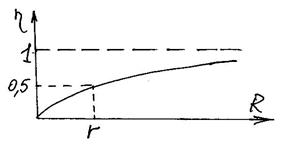
На графике зависимости КПД от 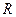видно, что максимум КПД достигается при , однако при этом абсолютная величина полезной мощности стремится к нулю.