А) Переходный процесс в электроприводе с двигателем постоянного тока независимого возбуждения при Lя¹0.
Рассмотрим схему на рис. 5.19. Отличительной особенностью схемы по сравнению с рассмотренными ранее является индуктивность Lя. Для якорной цепи справедливо уравнение:
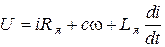 , (5.23)
, (5.23)
решив которое относительно w:
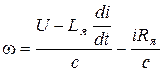 (*)
(*)
и обозначив 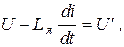 получим
получим
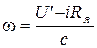 . (**)
. (**)
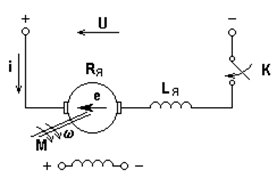
Рис. 5.19. Схема пуска электропривода постоянного тока с двигателем
независимого возбуждения
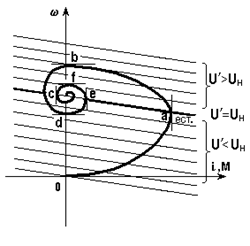
Если сравнить (**) с (3.4), то окажется, что уравнения идентичны, однако в (**) U¢ зависит от 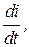 т.е. уравнение (**) представляет семейство прямых (рис. 5.20,а), параллельных естественной характеристике и располагающихся как ниже (
т.е. уравнение (**) представляет семейство прямых (рис. 5.20,а), параллельных естественной характеристике и располагающихся как ниже ( 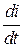 > 0), так и выше (
> 0), так и выше ( 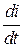 < 0) нее. При
< 0) нее. При 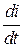 = 0, очевидно, уравнение (**) соответствует естественной характеристике.
= 0, очевидно, уравнение (**) соответствует естественной характеристике.
После замыкания ключа К ток i начинает расти, значит растет М и привод разгоняется (для упрощения рассуждений примем Мс = 0), переходя при этом с характеристики на на характеристику ( 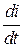 > 0, но уменьшается по мере разгона). В процессе увеличения тока и скорости (участок Оа на рис. 5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной характеристике, но М > Мс = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в Lя, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U¢, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = сw, причем в точке b i = 0 - запас энергии в Lя исчерпан, однако w >w0 и e > U, т.е. в якоре запасена избыточная механическая энергия.
> 0, но уменьшается по мере разгона). В процессе увеличения тока и скорости (участок Оа на рис. 5.20) возрастает запас энергии как в индуктивности, так и во вращающемся якоре. В точке а рост тока прекращается; при этом в соответствии с (*) привод оказывается на естественной характеристике, но М > Мс = 0. С точки а начинается спадание тока, т.е. энергия, запасенная в Lя, передается вращающемуся якорю. Механизм передачи очевиден из (*): напряжение, приложенное к якорю U¢, становится больше, чем напряжение сети U. На участке аb привод разгоняется, соответственно растет е = сw, причем в точке b i = 0 - запас энергии в Lя исчерпан, однако w >w0 и e > U, т.е. в якоре запасена избыточная механическая энергия.
а) б)
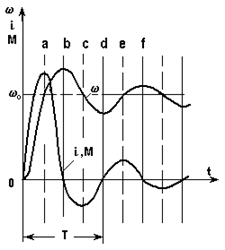
Рис. 5.20. Механические характеристики (а) и переходной процесс пуска при Lя ¹ 0 (б)
На участке bc под действием e > U ток изменяет направление, привод тормозится, при этом избыточная механическая энергия вновь переходит в электромагнитную энергию, накапливаемую в индуктивности. В точке с 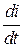 = 0, однако в Lя запасена энергия, чему соответствует i ¹ 0 и M ¹ 0. Привод продолжает тормозиться до точки d, затем процесс повторяется.
= 0, однако в Lя запасена энергия, чему соответствует i ¹ 0 и M ¹ 0. Привод продолжает тормозиться до точки d, затем процесс повторяется.
Кривая 0abcd... w0 в плоскости w - M представляет собою динамическую механическую характеристику. Соответствующие зависимости w(t), i(t) или M(t) показаны на рис. 5.20,б.
Так как в якорной цепи есть сопротивление Rя процесс перекачивания энергии сопровождается ее рассеиванием, вследствие чего система после ряда колебаний приходит в точку w0, соответствующую установившемуся режиму. Если бы сопротивление Rя было равным нулю, колебания w и М имели бы незатухающий характер. Если, наоборот, Rя велико, энергии, запасенной в Lя на участке 0а, может оказаться недостаточно для покрытия потерь в Rя и вывода якоря в точку w > w0 при i = 0. В этом случае процесс будет иметь апериодический характер.
Количественное описание рассмотренных выше процессов можно получить, решив совместно (5.1) и (5.23). Из (5.1) при Мс = 0 следует:
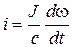 .
.
Подставив это выражение и его производную
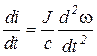
в (5.23), получим после элементарных преобразований:
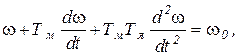 (5.24)
(5.24)
где
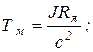
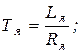
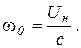
Решение (5.24) найдем в виде
w = wсв + wпр = 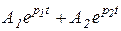 + w0, (5.25)
+ w0, (5.25)
где А1, А2 - постоянные, определяемые по начальным условиям
w½t=0 и 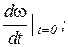
p1, p2 - корни характеристического уравнения
1 + Тмр + ТмТяр2 = 0 (D)
Решив (D), получим
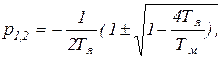
откуда вытекает условие колебательности процесса. Если
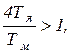 т.е. Тм < 4Тя,
т.е. Тм < 4Тя,
корни комплексные и процесс носит колебательный характер; если
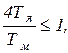 т.е. Тм ³ 4Тя,
т.е. Тм ³ 4Тя,
корни действительные и процесс апериодический.
Уравнение для тока или момента легко получить, воспользовавшись, как и прежде, (5.15). Продифференцировав (5.25) и умножив результат на J получим:
М = J ( 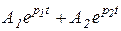 ). (5.26)
). (5.26)
Дата добавления: 2015-05-19; просмотров: 2281;
