Переходные процессы в системах

Рассмотренные ранее случаи переходных процессов относятся к простейшим электроприводам, когда учитываются лишь основные накопители энергии и можно уделять внимание физической стороне дела, относительно просто приходя к результату. Вместе с тем, все современные электроприводы представляют собой весьма сложные многоэлементные замкнутые системы, и для их анализа и синтеза приходится прибегать к приемам, разработанным в теории автоматического управления. Один из самых распространеных на практике приемов - использование структурных схем с передаточными функциями входящих в систему элементов.

Передаточная функция - отношение изображений по Лапласу выходной величины к входной при нулевых начальных условиях. Так, для цепи R - L, подключенной к источнику напряжения u(t) имеем:

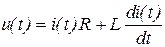
или, заменив 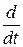на р, u(t) на u(p) и i(t) на i(p) и решив уравнение относительно i(p), принятом за выходную величину, получим

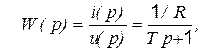
где 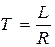- постоянная времени.

Для двигателя постоянного тока независимого возбуждения с учетом индуктивности якорной цепи L_я при питании якоря от источника напряжения u(t) и kФ = с, приняв за выходную величину w(t) и за входную u(t) после перехода к изображениям, получим для случая М_с = 0 структурную схему на рис. 5.25,а.

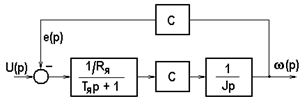
а)

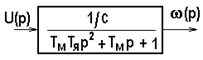
б) в)

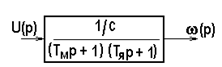
Рис.5.25. Передаточные функции двигателя постоянного тока

независимого возбуждения

Проделав элементарные преобразования, будем иметь передаточную функцию двигателя в виде колебательного звена (рис. 5.25,б):

,

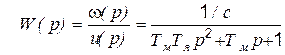где 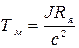- электромеханическая постоянная времени,

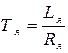- постоянная времени цепи якоря.

Если корни характеристического уравнения действительные, будем иметь два апериодических звена (рис. 5.25, в):

.

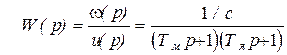Используя подобные действия, можно получить структурную схему любой системы и применить к ней приемы преобразования. анализа и синтеза, разработанные в теории автоматического регулирования.

Рассмотрим здесь кратко лишь один из таких приемов рационального управления динамической системой - построение систем подчиненного регулирования с последовательной коррекцией.

Для выходной координаты некоторого объекта регулирования образуют замкнутый контур, в который входит как сам объект, так и специальный регулятор, обеспечивающий заданное качество регулирования.

Пусть передаточная функция объекта регулирования имеет вид, к которому часто удается привести после преобразований передаточную функцию реального устройства:

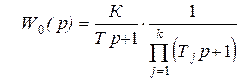, (5.31)

где К - общий коэффициент передачи,

Т - наибольшая постоянная времени,

Т_j - малые постоянные времени.

Поставим задачу максимально сократить время переходного процесса, исключив колебательность.

Рассмотрим сначала первый сомножитель в (5.31).

Теоретически возможно увеличить коэффициент передачи, включив на вход регулятор с передаточной функцией W_p(р)= K₁, однако это повысит чувствительность к помехам и склонность к колебательности. Теоретически возможен регулятор с передаточной функцией W_p(р)= Tр+1, однако такой регулятор нереализуем физически. На практике обычно используют пропорционально-интегральный регулятор (ПИ-регулятор) с передаточной функцией

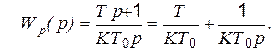(5.32)

Тогда в разомкнутой структуре с таким регулятором будем иметь без второго сомножителя в (5.31):

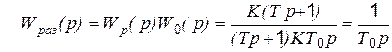. (5.33)

Для выбора Т₀ пользуются вторым сомножителем в (5.31). Если принять

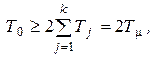(5.34)

то, как показано в теории, можно считать, что

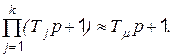(5.35)

Тогда, очевидно, передаточная функция разомкнутой системы будет

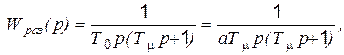(5.36)

а передаточная функция замкнутой системы определится как

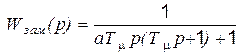, (5.37)

где 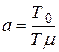- параметр, характеризующий вид переходного процесса; на рис. 5.26 приведены переходные функции для различных а. Очевидно, что компромисс между колебательностью и длительностью переходного процесса достигается при а = 2, и такая настройка (выбор Т₀) называется настройкой на технический оптимум. При этом без большой погрешности можно принять, что

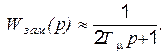(5.38)

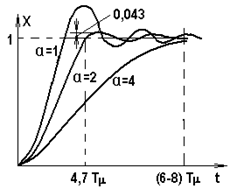
Рис. 5.26. Характер переходных процессов в контуре при

различных а = Т₀/Т_m

Итак, оптимизация объекта с передаточной функцией W₀(р) имеет компромиссный характер, осуществляется включением ПИ-регулятора W_р(р) с замыканием системы по выходной координате и состоит в замене разомкнутой структуры с большой постоянной времени Т замкнутой структурой с аналогичной передаточной функцией, но с другой постоянной времени, выбираемой из условия желаемого качества переходных процессов.

Изложенная процедура оптимизации особенно удобна и эффективна, если в систему входит несколько контуров - рис. 5.27. Начав с внутреннего (контур 1) и оптимизировав его, как было описано выше, переходят к следующему контуру (контур 2) и действуют аналогичным образом.

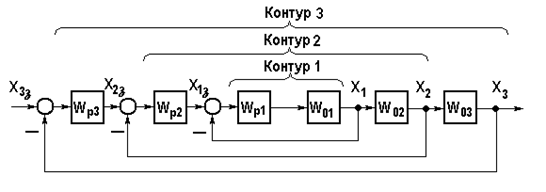
Рис. 5.27. Многоконтурная система

Если принять для упрощения, что малые постоянные Т_j, образовавшие некомпенсируемую постоянную Т_m, сосредоточены во внутреннем контуре, а во внешнем отсутствуют, можно получить следующие передаточные функции i-ого контура:

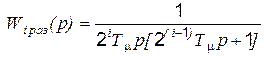(5.39)

и

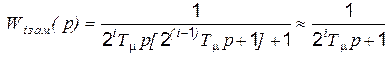. (5.40)

К достоинствам изложенной оптимизации относится идентичность переходных процессов в каждом контуре при их независимой настройке, простота ограничения координат за счет ограничения задания нелинейной характеристикой вход-выход соответствующего регулятора, удобство в практической наладке систем. К недостаткам можно отнести сравнительно низкое быстродействие внешних контуров - см. (5.40).

Приведенный пример оптимизации сложной системы, разумеется, далеко не исчерпывает всех возможностей. Так, в настоящее время с появлением эффективной компьютерной поддержки все чаще используется прием, состоящий в составлении поэлементного математического описания системы, представлении дифференциальных уравнений в форме Коши и использовании мощных пакетов типа Simnon, Simulink и др. для работы с полученным математическим описанием. Самым сложным, требующим немалых усилий здесь является этап получения адекватного математического описания. Остальное берет на себя мощный, хорошо организованный программный продукт.

Во всех подходах, естественно, теряется физическая сторона процессов, однако появляется возможность работать с весьма сложными системами.