Закон Ома для неоднородного участка цепи. Любой участок цепи, НЕ содержащий источника ЭДС, называют однородным; участок цепи, содержащий источник ЭДС – неоднородным.

Любой участок цепи, НЕ содержащий источника ЭДС, называют однородным; участок цепи, содержащий источник ЭДС – неоднородным.

Ограничимся практически важным случаем, когда цепь состоит из резисторов, источников тока и соединительных проводов.

Сначала обобщим локальный закон Ома. Если на участке цепи действуют не только электрические, но и сторонние силы, плотность тока пропорциональна их векторной сумме:

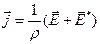. (1)

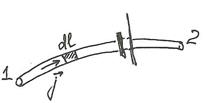
Рассмотрим неоднородный участок 1-2. Умножаем скалярно обе обобщенного закона Ома (1) на 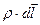и интегрируем по трубке тока от сечения 1 до сечения 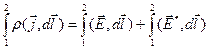2:

. (2)

Поскольку перемещение 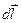направлено вдоль вектора плотности тока 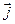, 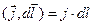. Плотность тока выражаем через силу тока I (одинаковую в любом сечении участка цепи) и площадь сечения 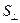: 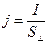. Тогда интеграл в левой части (2) равен:

.

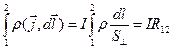Интегралы в правой части (2) определяют, соответственно, разность потенциалов и ЭДС:

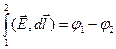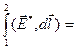; Е,

и мы получаем из (2):

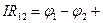Е

Это и есть закон Ома для данного неоднородного участка. Такой участок изображается следующей схемой:

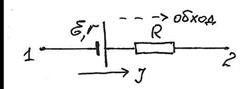
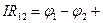Е

Если источник ЭДС на участке 1-2 включен в противоположном направлении, так что, двигаясь от 1 к 2, мы проходим его от положительного полюса к отрицательному, то работа сторонних сил меняет свой знак: 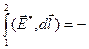Е, и закон Ома принимает вид:

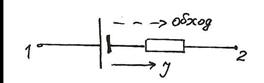
Е

А если мы обходим участок 1-2 против направления тока, то , и закон Ома принимает вид:

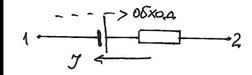
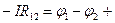Е

Итак, в общем случае можно символически записать закон Ома для неоднородного участка цепи так:

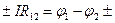Е (3).

Знаки плюс или минус соотносятся с направлением обхода участка:

· При обходе участка ПО ТОКУ: 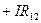. Против тока, соответственно, .

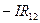· При обходе источника от положительного полюса к отрицательному (т.е. в том направлении, в котором этот источник сам давал бы ток): + Е. При обходе в противоположном направлении, соответственно, –Е.

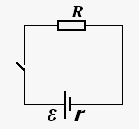
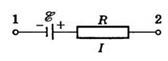
Сформулируем теперь закон Ома для полной неразветвленной цепи, которая схематически изображается так:

Обойдем цепь по току. Начальная и конечная точки совпадают, поэтому 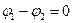, и мы получаем: 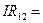Е. Полное сопротивление цепи есть сумма сопротивления R внешнего участка и внутреннего сопротивления r источника: . Поэтому для замкнутой цепи

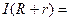Е (4).