Разветвленные цепи. Правила Кирхгофа

Эти правила позволяют рассчитать силы тока в любых разветвленных цепях.

1-ое правило. Алгебраическая сумма токов в каждом узле цепи равна нулю:

.

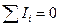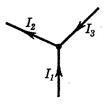
Токи, втекающие в узел, берутся со знаком «плюс», вытекающие из узла – со знаком «минус». Для узла, изображенного на рисунке:

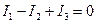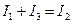, или (сумма втекающих токов равна сумме вытекающих).

Это правило – следствие уравнения непрерывности для стационарных токов: заряд не может накапливаться в узлах.

2-ое правило. Для любого замкнутого контура, выделенного в цепи, алгебраическая сумма произведений сил токов на отдельных участках на сопротивления этих участков равна алгебраической сумме ЭДС в контуре:

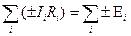
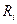( – суммарное сопротивление i-той ветви).

Правило знаков здесь такое же, как в законе Ома для неоднородного участка цепи.

2-ое правило Кирхгофа следует из закона Ома. Докажем его. Выделим некоторый замкнутый контур в цепи и направление его обхода. Для каждого последовательного участка контура (от одного узла до другого) укажем направление тока, введем его обозначение и запишем закон Ома в соответствии с правилом знаков. Получим систему уравнений (сколько последовательных участков в контуре, столько и уравнений – для нашего рисунка три):

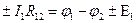
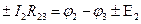
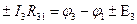
Здесь 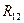– полное сопротивление участка между узлами 1 и 2, включающее и внутреннее сопротивление источника на этом участке, и т. д.

Сложив все уравнения, придём ко второму правилу, т.к. все потенциалы в правой части суммарного уравнения сократятся.

Замечания.

Число полученных уравнений должно совпадать с числом искомых токов, т.е. с числом последовательных участков цепи. При этом надо следить, чтобы одни из полученных уравнений не оказались линейной комбинацией других. Для этого учтите два факта:

1) Если в цепи всего N узлов, то независимых уравнений для токов будет .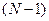

2) Если в цепи можно выделить несколько контуров, то независимые уравнения получатся только для тех контуров, которые не являются объединением уже рассмотренных.

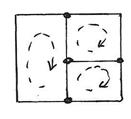
Например, в этой цепи всего 4 узла – значит, первое правило можно записать для любых трех из них.

Линейно независимые уравнения можно записать для трех контуров – например, отмеченных стрелками.

Всего получится 3+3=6 уравнений, что равно числу последовательных участков этой цепи.

Сформулируем общий алгоритм расчета токов в разветвленной цепи.

1) Обозначить стрелками предполагаемые направления токов на всех последовательных участках цепи и ввести обозначения этих токов. (Не бойтесь ошибиться с направлением тока: если в итоге для этого тока будет получено отрицательное числовое значение, значит, он течет в противоположном направлении, но числовое значение остается верным).

2) Отметить все узлы и записать 1-ое правило для всех, кроме одного.

3) Выделить все независимые контуры и выбрать направление обхода для каждого из них; указать эти направления стрелками. Записать 2-ое правило для каждого контура.

4) Записав все уравнения, убедитесь, что их число совпадает с числом неизвестных токов.

Если требуется решить систему более чем из 4-х уравнений, используйте правила Крамера (см. решение задачи 5.73)