Описание колебаний сложных молекул. Классификация нормальных колебаний.
Из приближения Борна-Опенгеймера следующий вид:

В этом уравнении 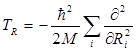 - оператор кинетической энергии ядер, ε® – электронная энергия как функция ядерных координат, E – энергия системы. В гармоническом приближении электронная энергия разлагается вблизи положения равновесия:
- оператор кинетической энергии ядер, ε® – электронная энергия как функция ядерных координат, E – энергия системы. В гармоническом приближении электронная энергия разлагается вблизи положения равновесия:
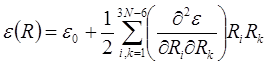
В нормированных нормальных координатах
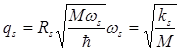 , кинетическая и потенциальная энергии имеют вид:
, кинетическая и потенциальная энергии имеют вид:
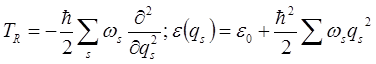
Тогда уравнение (2.1) превращается в уравнения для гармонических осцилляторов:
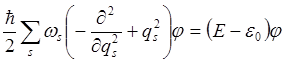 (2.2)
(2.2)
Полная волновая функция системы представляет собой произведение функций, описывающих гармонические колебания по каждой координате. Полная энергия является суммой энергий отдельных колебаний:
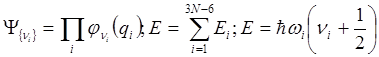 ???(2.3)
???(2.3)
В соотношениях (2.3) знаком {νi} обозначен набор чисел, показывающий, какое число квантов i-го нормального колебания возбуждено; 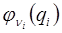 – волновая функция гармонического осциллятора, у которого возбуждено νi квантов:
– волновая функция гармонического осциллятора, у которого возбуждено νi квантов:
 (2.4)
(2.4)
Функции 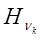 обозначают полиномы Эрмита νk порядка.
обозначают полиномы Эрмита νk порядка.
Рассмотрим теперь классификацию нормальных колебаний (колебательных волновых функций). Она проводится аналогично классификации энергетических уровней и волновых функций в случае электронных спектров.
Нормальные координаты колебаний данной частоты образуют базис неприводимых представлений группы симметрии данной молекулы. Если размерность базиса неприводимого представления больше единицы и равна k , то данной частоте соответствует k нормальных колебаний (частота вырождена, k – степень вырождения).
Таким образом, из симметрии молекулы (таблицы характеров неприводимых представлений) можно определить, по каким представлениям преобразуются нормальные координаты (волновые функции) различных колебаний. Такую классификацию можно привести следующим образом.
Пусть мы имеем молекулу, содержащую N ядер. Найдем характер представления, по которому преобразуются смещения ядер из положения равновесия. Это представление называют механическим представлением. Сопоставим каждому ядру i набор смещений (xi,yi,zi) из положения равновесия. Найдем характер матрицы преобразования следующего столбца:
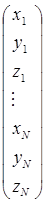 (2.5)
(2.5)
Выясним, как будет преобразоваться столбец (2.5) под действием преобразований пространства, оставляющих неизменной данную молекулу.
А) Тождественное преобразование Е.
При этом все смещения переходят сами в себя. Характер этого преобразования равен сумме диагональных элементов единичной матрицы, т.е. χ(E)=3N.
Б) Поворот молекулы на угол φ – Сφ. Пусть при этом Nφ ядер остаются на месте. Только координаты этих ядер нужно учитывать при вычислении характера матрицы, описывающей это преобразование. Их теории групп известно, что повороты вокруг разных осей на равные углы относятся к одному классу и имеют одинаковые характеры, поэтому ось поворота мы можем выбрать произвольно, из соображений простоты. Пусть для ядра i , одного из тех ядер, которые остались на своих местах, ось координат z совпадает с осью поворота на угол φ. Тогда матрица преобразований координат (смещений) для этого неподвижного ядра имеет вид:

 ????(2.6)
????(2.6)
Учитывая все Nφ ядер, оставшихся на месте после поворота, получим следующую формулу для характера этого преобразования
 ????(2.7)
????(2.7)
В) Отражение в плоскости σ. Пусть при этом Nσ ядер остаются на месте. Выберем в качестве плоскости плоскость 0XY.
Тогда матрица преобразования координат для неподвижного ядра имеет вид:
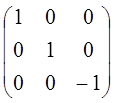
Учитывая, что Nσ ядер остаются на месте, получим следующий характер матрицы преобразования, описывающего отражения
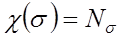 (2.8)
(2.8)
Г) Инверсия. При этой операции на месте остаются  ядер. Матрица преобразования одного ядра имеет вид:
ядер. Матрица преобразования одного ядра имеет вид:
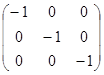
Для всей молекулы характер преобразования, описывающего инверсию, равен:
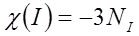 ????(2.9)
????(2.9)
Таким образом, мы можем найти характер механического представления, описывающего смещения ядер молекулы.
В механическое представление входят характеры представлений, соответствующих трансляционному (Tx,Ty,Tz), вращательному (Rx,Ry,Rz) и искомому колебательному движению. Характеры матриц, соответствующих этим движениям, мы будем обозначать χT , χR , χv .
Таким образом
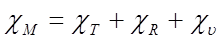 (2.9)
(2.9)
Поэтому для получения характера колебательного движения необходимо из характера механического движения вычесть характеры трансляционного и вращательного движений. Обычно эти характеры приводятся в таблицах характеров неприводимых представлений соответствующей группы симметрии, в противном случае их находят из геометрических соображений.
В качестве примера рассмотрим классификацию нормальных колебаний молекулы воды. Введем оси координат следующим образом
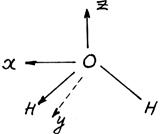 |
Молекула Н2О лежит в плоскости xz. Таблица характеров неприводимых представлений группы С2v , к которой принадлежит молекула воды, имеет вид:
Таблица 2
| E | C2 | σv(x,z) | σv΄(y,z) | |||
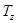
| 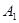
| |||||
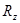
| 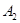
| -1 | -1 | |||
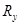
| 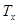
| 
| -1 | -1 | ||
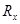
| 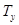
| 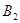
| -1 | -1 | ||

| -1 | |||||
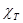
| -1 | |||||
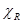
| -1 | -1 | -2 | |||
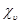
|
В таблице 2 представлены также характеры механического, трансляционного и вращательного представлений. Рассмотрим, как был получен характер механического представления. В молекуле воды существует 3N – 6=3 нормальных колебаний. Характер матриц механического представления для отдельных операций симметрии имеют вид:
Согласно формулам (2.6-2.8):
 ; ????
; ????
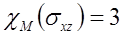 ; ?????
; ?????
Разлагая представления Гv, отвечающее колебательному движению, на неприводимые представления, получим:
 (2.10)
(2.10)
На основании (2.10) мы заключаем, что у молекулы воды есть 3 невырожденных колебания: два полносимметричных и одно неполносимметричное. Эти колебания и соответствующие нормальные координаты имеют следующий вид.
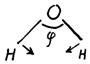 1)
1) 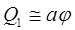
(кислород из-за большой массы смещается мало)
δ(s)=1595 см-1
Знак δ обозначает деформационное колебание, при котором в основном изменяется величина угла между связями; знак s обозначает симметричное колебание А1.
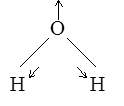
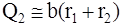
(кислород смещается мало)
Знак V обозначает так называемое валентное колебание, при котором в основном меняются длины связей.
Как правило, частоты валентных колебаний больше, чем частоты деформационных.
3)

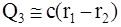
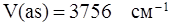
Знак as в скобках обозначает антисимметричное колебание.
Схема нижних энергетических уровней молекулы воды выглядит следующим образом:
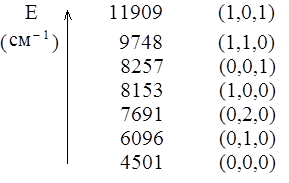
На этой схеме колебательный уровень обозначается как (V1, V2, V3). Здесь V1 – число квантов с частотой ω1=3652 см‑1, V2 – с частотой ω2=1595 см‑1, V3 – с частотой ω3=3756 см‑1.
Дата добавления: 2015-06-10; просмотров: 2153;
