СТЕПЕНЬ ПОДВИЖНОСТИ МЕХАНИЗМОВ
В простейшей интерпретации: механизм – это кинематическая цепь + двигатель.
Все механизмы можно разделить на плоские и пространственные. У плоского механизма точки его звеньев описывают траектории, лежащие в одной или параллельных плоскостях. У пространственного механизма точки его звеньев описывают неплоские траектории или траектории, лежащие в пересекающихся плоскостях.
На рисунке 1.2 изображен плоский шарнирный четырехзвенный механизм, а на рисунке 1.3 – плоский механизм двухступенчатого редуктора. На рисунке 1.4 показан пространственный механизм зажима. На рисунке 1.5 изображена пространственная зубчатая передача, образованная коническими колесами.
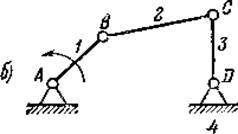
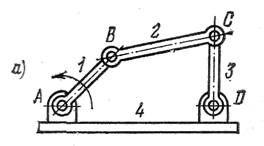
а – полуконструктивная схема; б – кинематическая схема
Рисунок 1.2 - Плоский шарнирный четырехзвенный механизм
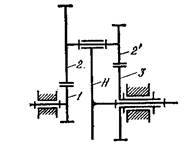
Рисунок 1.3 - Двухступенчатый редуктор с цилиндрическими
зубчатыми колесами
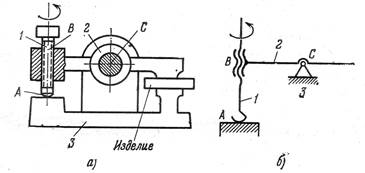
а - полуконструктивная схема; б - кинематическая схема
Рисунок 1.4. – Пространственный механизм зажима
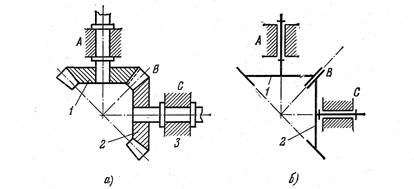
а - полуконструктивная схема; б - кинематическая схема
Рисунок 1.5. – Зубчатая передача с коническими колесами
Число степеней подвижности W замкнутой кинематической цепи с одним неподвижным звеном можно найти, воспользовавшись структурными формулами, которые для различных механизмов имеют следующий вид:
для пространственных механизмов (формула П.И. Сомова – А.П. Малышева):
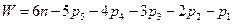 ; (1.1)
; (1.1)
для плоских механизмов (формула П.Л. Чебышева):
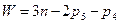 ; (1.2)
; (1.2)
для механизмов, состоящих из поступательных кинематических пар (формула В.В. Добровольского):
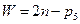 . (1.3)
. (1.3)
В этих формулах W – степень подвижности механизма, n – число подвижных звеньев, p5, p4, p3, p2, p1 – число кинематических пар соответствующих классов. Так, например, p5 – число кинематических пар V класса (одноподвижная кинематическая пара), p4 – число кинематических пар IV класса (двухподвижная кинематическая пара) и т.д. При этом необходимо учитывать, что количество W указывает на число ведущих звеньев, которые обозначаются на схемах стрелками.
На рисунке 1.6 показан механизм, который надо отнести к плоскому, так как на движения его звеньев наложены по три общих условия связи: звенья не могут перемещаться поступательно вдоль оси Ox и вращаться вокруг осей Oy и Oz.
Прежде чем применять структурные формулы, следует установить, сколько общих условий связи наложено на движение звеньев исследуемого механизма. Также следует выяснить, нет ли в данном механизме звеньев, которые накладывают пассивные (избыточные) связи или вносят лишние степени свободы, не влияющие на кинематику основных звеньев механизма.
Избыточные связи определяются по формуле
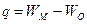 , (1.4)
, (1.4)
где WM – степень подвижности действующего механизма, WO - степень подвижности основного механизма. Причем степень подвижности основного механизма определяется по формулам (1.1) и (1.2), тогда избыточные связи q можно определить из соотношений
для пространственных механизмов:
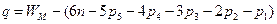 ; (1.5, а)
; (1.5, а)
для плоских механизмов:
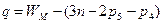 . (1.5, б)
. (1.5, б)
Степень подвижности WM определяется по количеству ведущих звеньев.
|
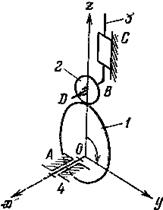
Рисунок 1.6. - Плоский кулачковый
механизм
Если ролик жестко связать с толкателем, то от этого закон движения толкателя, очевидно, не изменится. Круглый ролик, свободно поворачивающийся вокруг своей оси, вносит в механизм лишнюю степень свободы, т.е. он будет обладать местной подвижностью, и при подсчете степени подвижности механизма это вращательное движение принимать во внимание не должно.
Считая, что ролик жестко связан с толкателем, подсчитываем степень подвижности механизма по формуле (1.2):
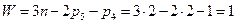 .
.
Формальный же подсчет привел бы нас к такому результату:
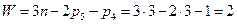 .
.
Рассмотрим на примере определение избыточных связей q.
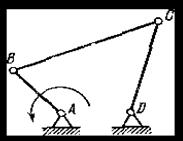
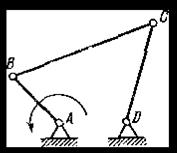
Пример 1. На рисунке 1.7, а изображен плоский рычажный коромысловый механизм (шарнирный четырехзвенник). Определить количество избыточных связейq.
|
|
|
|
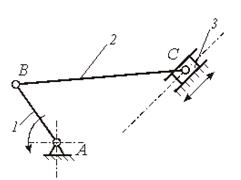
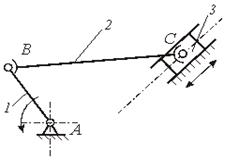
Рисунок 1.7. – К определению избыточных связей
Степень подвижности действующего механизма WМ=1 (по количеству ведущих звеньев). Тогда по формуле 1.5, а имеем
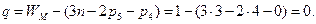
Добавим звену DC дополнительное вращение (рисунок 1.7, б). При этом степень подвижности станет WМ=2. Тогда
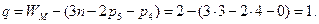
Пример 2. На рисунке 1.7, в изображен плоский рычажный кривошипно-ползунный механизм. Определить количество избыточных связей q.
АналогичноПримеру 1 имеем
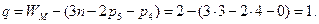
Если шатун 2 соединить сферическими парами В и С (рисунок 1.8, д) с ползуном и кривошипом, то появится одна местная подвижность – вращение шатуна относительно своей продольной оси (рисунок 1.7, г). Тогда количество избыточных связей действующего механизма будет
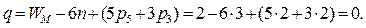
Дата добавления: 2015-06-01; просмотров: 8268;
