О неточности задания сил в классической механике

Согласно исходным постулатам причинной механики причина и следствие всегда разделены сколь угодно малыми, но не равными нулю пространственным δx и временнм δt различиями (причем временное различие имеет определенный знак в связи с тем, что следствие наступает позже причины). Отношение данных величин названо Н. А. Козыревым ходом времени и обозначено через с₂:

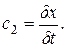(4.1)

Классическая механика тоже содержит положение о пространственном неналожении причины и следствия. Оно вытекает из III закона Ньютона, в соответствии с которым сила действия и сила противодействия приложены к разным телам, что обязательно означает наличие ненулевого пространственного расстояния между точками приложения сил. Вместе с тем, классическая механика не учитывает существование временнго различия между причиной и следствием. Это видно также из III закона Ньютона, согласно которому силы, приложенные к причине и следствию, действуют в один и тот же момент времени. Таким образом, можно сказать, что классическая механика является вырожденным случаем причинной механики, отвечающим следующим значениям величин: δx ≠ 0, δt = 0 и с₂ = ∞ [1].

Пренебрежение временным различием между причиной и следствием приводит к неточности задания направлений и абсолютных значений сил в классической механике. Покажем это.

Примем в качестве геометрического образа пространства и времени четырехмерное собственно евклидово пространство (такая модель, как известно, не противоречит классической механике Ньютона). Поскольку все четыре координаты в этом пространстве должны измеряться в одних единицах, положим по аналогии с тем, как делается в теории относительности, что временная координата есть ct, где c – скорость света в вакууме, t – время.

В настоящем разделе мы будем интерпретировать величины | 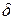x| и | 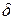t| иначе, чем делали это в разд. 1. Будем считать их величинами детерминированными, то есть принимающими для каждого конкретного причинно-следственного звена вполне определенные значения, которые, однако, могут быть различными для разных звеньев. Именно такая трактовка данных величин используется в работах Н. А. Козырева (о чем, правда, можно судить, лишь из контекста, так как в [1] этот вопрос детально не обсуждается). Будем полагать выполненным закон Козырева

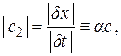(4.2)

где 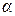– постоянная тонкой структуры ( 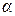» 1/137). Подчеркнем, что ниже мы сосредоточим внимание на «классических» силах, а к обсуждению добавочных сил, которые рассматривались в разд. 3, вернемся только в конце настоящего раздела.

То обстоятельство, что причина и следствие проявляются в различные моменты времени, означает принадлежность их различным гиперплоскостям одномоментных событий (рис. 4.1). В связи с этим сразу встает вопрос: «Куда направлены силы, приложенные к причине и следствию: лежат они в соответствующих гиперплоскостях одномоментных событий или направлены вдоль прямой, соединяющей точку-причину и точку-следствие?» Классическая механика не позволяет сделать выбор между такими возможностями. Поэтому воспользуемся соображениями симметрии. В связи с тем, что причинно-следственное звено имеет в качестве элемента симметрии ось вращения, проходящую через составляющие его точки, естественно ожидать, что и система сил, связанных с ним, обладает той же симметрией. Это дает основание полагать, что силы взаимодействия направлены вдоль прямой, соединяющей причину и следствие, как показано на рис. 4.1. Такая ориентация сил отвечает и релятивистской симметрии пространства и времени. (Отметим, что приведенное рассуждение не относится к добавочным силам, введенным в разд. 3, потому что симметрия последних определяется свойствами не только причинно-следственного звена, но и времени.)

Рис. 4.1. Причина П и следствие С при осуществлении причинного

взаимодействия

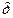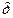F – сила взаимодействия причины и следствия; F_в – составляющая силы F вдоль оси времени; F_г– составляющая силы F вдоль гиперплоскости одномоментных событий; | x|, | t| – пространственное и временное расстояния между причиной и следствием при осуществлении причинного взаимодействия; τ – ось времени; Γ₁, Γ₂ – гиперплоскости одномоментных событий, проходящие через соответственно точку-причину П и точку-следствие С; М_пП – мировая линия причины (показана только ее часть до момента времени t); М_сМ_с′– мировая линия следствия; C₀ –точка пересечения мировой линии следствия с гиперплоскостью Γ₁; C′ – проекция точки-следствия С на Γ₁; c – скорость света в вакууме; здесь учтено, что следствие наступает позже причины; гиперплоскости Γ₁ и Γ₂ изображены с понижением размерности на единицу.

При указанном направлении сил взаимодействия они имеют ненулевую составляющую вдоль оси времени, что не учитывается классической механикой. Найдем связь этой составляющей с составляющей тех же сил, лежащей в гиперплоскости одномоментных событий. Воспользовавшись тем обстоятельством, что при проецировании на гипер-плоскость прямая переходит в прямую, нетрудно заключить, что вектор силы взаимодействия F и обе его составляющие, о которых идет речь, лежат в (двухмерной) плоскости, проходящей через три точки — точку-причину П, точку-следствие С и точку C′ (где C′ — проекция точки С на соответствующую точке П гиперплоскость одномоментных событий). При этом одна из составляющих вектора F перпендикулярна, а другая параллельна отрезку ПC′. С учетом данного факта из рис. 4.1 можно видеть, что составляющая F_в, направленная вдоль оси времени, и составляющая F_г, направленная вдоль гиперплоскости одномоментных событий, связаны зависимостью

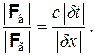
Отсюда, используя закон (4.2), находим

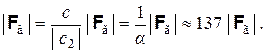(4.3)

Итак, принятие условия 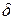t≠ 0, вообще говоря, может приводить к появлению у сил взаимодействия временнй составляющей. Одна из неточностей задания сил в классической механике состоит как раз в неучете такой возможности.

Разумеется, использованное нами утверждение о том, что силы взаимодействия направлены именно вдоль прямой, соединяющей причину и следствие, является всего лишь гипотезой. Возможны и другие варианты. Например, если подобно тому, как это делается в теории относительности, определять силу как производную импульса по времени, то она обязательно будет лежать в гиперплоскости одномоментных событий, потому что в ней лежит вектор импульса. Вместе с тем, до тех пор, пока вопрос о действительном направлении сил взаимодействия окончательно не решен, необходимо учитывать возможность присутствия у сил временной составляющей.

В классической механике неточность задания сил проистекает еще и из-за неучета взаимного смещения причины и следствия, которое происходит за промежуток времени 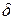t. Оценим эту неточность.

Принятое в классической механике допущение о совпадении моментов проявления причины и следствия означает, что точками приложения сил взаимодействия считаются точки мировых линий причины и следствия, находящиеся в одной гиперплоскости одномоментных событий. При 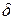t≠ 0 в качестве такой гиперплоскости может быть выбрана любая, располагающаяся между гиперплоскостью, проходящей через точку-причину, и гиперплоскостью, проходящей через точку-следствие (обе показаны на рис. 4.1). Проанализируем две крайние ситуации, когда именно эти гиперплоскости служат в качестве гиперплоскости одномоментных событий, рассматриваемой в классической механике (рис. 4.2).

Рис. 4.2. Проекции причинно-следственного звена

на гиперплоскости одномоментных событий, проходящие через точку-причину П (а) и точку-следствие С (б)

F_г — составляющая силы взаимодействия причины и следствия, направленная вдоль гиперплоскости одномоментных событий; F_кл — сила, рассматриваемая в классической механике; ψ₁, ψ₂ — углы между векторами сил F_г и F_кл; С₀ — точка пересечения мировой линии следствия с гиперплоскостью одномоментных событий, проходящей через точку-причину П; C′ — проекция точки-следствия С на ту же гиперплоскость; П₀ — точка пересечения мировой линии причины с гиперплоскостью одномоментных событий, проходящей через точку-следствие С; П′ — проекция точки-причины П на ту же гиперплоскость; | 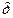x|, | 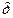t| — пространственное и временное расстояния между причиной П и следствием С при осуществлении причинного взаимодействия; u_с, u_с^||, u_с^┴ — вектор скорости следствия и его составляющие, параллельная и перпендикулярная силе F_г; u_п, u_п^||, u_п^┴ — то же для причины; i — орт линии действия силы F_г, направленный от точки П (или П′ ) к точке C′ (или С).

Из рисунка непосредственно видно, что из-за взаимного перемещения причины и следствия отрезок, соединяющий одномоментные точки их мировых линий, имеет в данных двух ситуациях как разное направление, так и разную длину (на рис. 4.2,а это есть отрезок ПС₀, на рис. 4.2,б – отрезок П₀С). Сила взаимодействия, рассматриваемая в классической механике, направлена как раз вдоль данного отрезка и однозначно определяется его длиной. На рисунке она обозначена через F_кл. Вместе с тем составляющая F_г действительной силы взаимодействия F имеет иное направление – вдоль отрезка, соединяющего проекции точки-причины П и точки-следствия С на гиперплоскость одномоментных событий (на рис. 4.2,а и б соответственно ПC′ и П′С). Отметим, что линия действия составляющей F_г является одной и той же при любом направлении силы взаимодействия F в плоскости ПСС′ (см. рис. 4.1), в частности, и в том случае, когда сила F не имеет временной составляющей, то есть при F = F_г. Следует отметить также, что системы векторов, изображенные на рис. 4.2,а и на рис. 4.2,б, могут располагаться в четырехмерном пространстве-времени в плоскостях, которые не параллельны друг другу; однако принадлежащие этим плоскостям прямые, помеченные на рисунках ортом i, параллельны между собой.

Оценим вначале неточность направления силы F_кл. При этом временно пренебрежем неточностью ее абсолютного значения.

Допустим, что ускорения взаимодействующих точек столь малы, что участки мировых линий, проходимые ими за промежуток времени 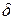t, близки к прямолинейным. Тогда проекции этих участков (то есть линии С₀С′ и П′П₀ на рис. 4.2) также близки к прямолинейным. В таком случае углы ψ₁ и ψ₂ между силами F_г и F_кл в двух анализируемых ситуациях, как легко убедиться, удовлетворяют выражениям

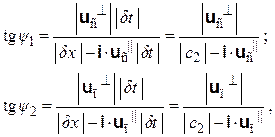(4.4)

где u_с^┴, u_с^|| — составляющие скорости движения следствия, соответственно перпендикулярная и параллельная силе F_г; u_п^┴, u_п^|| — то же для причины; i — единичный вектор, лежащий на линии действия силы F_г и направленный от точки П к точке С′ (на рис. 4.2,а) или от П′ к С (на рис. 4.2,б); здесь использован закон (4.2); все скорости определяются по отношению к некоторой инерциальной системе координат.

Будем считать, что скорости движения следствия u_с и причины u_п малы по сравнению с константой c₂: |u_с| << |c₂|, |u_п| << |c₂|. Тогда на основании (4.4) можем записать (в линейном по |u_с|/|c₂| и |u_п|/|c₂| приближении)

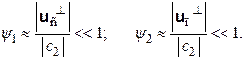(4.5)

В этом случае разность сил F_г – F_кл приближенно описывается следующими выражениями для двух рассматриваемых ситуаций в предположении, что длины векторов F_г и F_кл примерно равны (см. рис. 4.2):

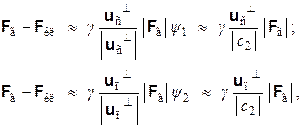(4.6)

где γ = sign(F_г ∙ i), коэффициент γ равен +1 или –1 в зависимости от того, взаимодействуют причина и следствие силами отталкивания (F_г ∙ i > 0) или притяжения (F_г ∙ i < 0); множители u_с^┴/|u_с^┴| и u_п^┴/|u_п^┴| играют роль орта, задающего направление силы F_г – F_кл.

Из зависимостей (4.6) вытекает, что для компенсации неточности направления действия силы F_кл необходимо прибавить к ней добавочную силу F_^, равную в среднем

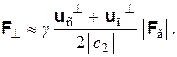(4.7)

Из тех же зависимостей (4.6) следует, что крайние положения силы F_кл, изображенные на рис. 4.2,а и б, различаются на величину ΔF_кл^┴, равную

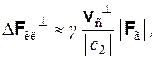(4.8)

где v_с^┴ — перпендикулярная силе F_г составляющая вектора v_с скорости движения следствия относительно причины (v_с = u_с – u_п). Отметим, что величина ΔF_кл^┴ имеет инвариантный характер, так как она определяется относительной скоростью движения причины и следствия, в то время как величина F_^, вследствие зависимости ее от скоростей, определяемых по отношению к используемой системе координат, зависит от выбора этой системы координат и поэтому не инвариантна.

Теперь оценим неточность задания абсолютного значения силы F_кл (пренебрегая неточностью ее направления).

Рассмотрим типичный закон взаимодействия, когда модуль силы обратно пропорционален квадрату расстояния между взаимодействующими материальными точками:

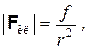(4.9)

здесь f обозначает все входящие в закон величины, кроме расстояния. Согласно постулатам причинной механики пространственное расстояние между причиной и следствием при осуществлении взаимодействия есть | 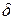x|. Между тем, в двух изображенных на рис. 4.2 ситуациях расстояния r₁ и r₂ между точками приложения «классических» сил (то есть длины отрезков ПС₀ и П₀С) отличны от |δx| и составляют

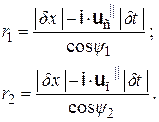(4.10)

В случае |u_с| << |c₂|, |u_п| << |c₂|, как следует из выражений (4.5), имеют место приближенные равенства cos ψ₁ ≈ 1, cos ψ₂ ≈ 1 (верные в линейном приближении по |u_с|/|c₂|, |u_п|/|c₂| ). Учитывая это и закон (4.2), получаем из равенств (4.10) следующие значения r₁ и r₂:

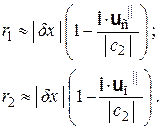(4.11)

Подстановка этих значений расстояния в закон (4.9) дает для двух анализируемых ситуаций такие значения модуля силы:

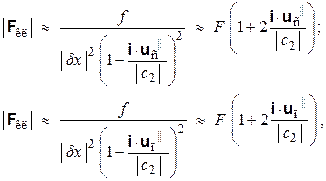(4.12)

где F = f / | 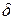x|² — действительное значение модуля «классической» силы взаимодействия.

Из выражений (4.12) следует, что для компенсации неточности в задании модуля силы F_кл нужно прибавить к ней добавочную силу F_||, составляющую в среднем

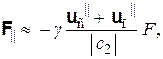(4.13)

где учтено, что векторы i, u_с^||, u_п^||, F_г параллельны между собой и приближенно параллельны вектору F_кл. Из выражений (4.12) вытекает также, что размах значений модуля силы F_кл в двух анализируемых ситуациях таков, что соответствующая ему разностная сила ΔF_кл^|| равна

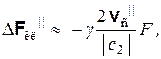(4.14)

где v_с^|| – параллельная силе F_г составляющая вектора v_с скорости движения следствия относительно причины. Здесь аналогично тому, как это имело место ранее, сила ΔF_кл^|| является инвариантной величиной, а сила F_|| не является таковой.

При практическом использовании формул (4.7), (4.8), (4.13), (4.14) удобно выражать задаваемые ими силы через среднее значение «классической» силы. Далее именно это среднее значение будем обозначать символом F_кл. В связи с тем, что указанные силы малы в сравнении с F_кл, полученные формулы останутся справедливыми (в рассмат-риваемом линейном приближении по |u_с|/|c₂|, |u_п|/|c₂| ), если заменить в них действительные силы их приближенным «классическим» значением, а также считать, что входящие в них составляющие скоростей, помеченные значками ^ и ||, направлены соответственно перпендикулярно и параллельно не силе F_г, а силе F_кл. Производя указанные изменения, заключаем на основании формул (4.8) и (4.14), что разность между анализируемыми крайними значениями «классической» силы может быть представлена в виде суммы следующих двух составляющих, первая из которых перпендикулярна, а вторая параллельна силе F_кл:

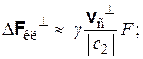(4.15)

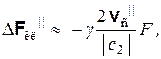(4.16)

где γ = sign(F_кл ∙ i); F = |F_кл|. А на основании формул (4.7), (4.13) приходим к выводу, что добавочные силы, которые необходимо прибавить к «классической» силе F_кл для компенсации неточностей ее направления и абсолютного значения, имеют вид

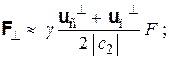(4.17)

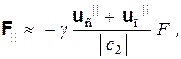(4.18)

причем первая из этих сил перпендикулярна, а вторая параллельна силе F_кл. Напомним, что при выводе формул (4.16) и (4.18) использован закон взаимодействия (4.9).

Присоединим сюда формулу для временнй составляющей силы взаимодействия, о которой шла речь ранее. Из выражения (4.3) легко получаем, что

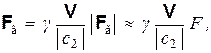(4.19)

где V – «скорость» движения нашего Мира вдоль оси времени (вектор V параллелен оси времени, направлен из прошлого в будущее и имеет модуль c: |V| = c); здесь учтено, что вектор F_в при отталкивающем характере взаимодействия направлен в ту же сторону, что и V, а при притягивающем – в противоположную сторону (см. рис. 4.1).

Таким образом, в классической механике, из-за неучета временного различия между моментами проявлений причины и следствия, сила взаимодействия оказывается заданной не точно. Погрешности имеют ее составляющие по трем взаимно перпендикулярным направлениям: по оси времени и по двум направлениям, лежащим в гиперплоскости одномоментных событий, — вдоль самой силы и перпендикулярно к ней.

В разд. 3 обсуждалась еще одна неточность «классической» силы, которая обусловлена специфическим воздействием времени. Выпишем все четыре добавки, компенсирующие неточности «классических» сил, применительно к частному случаю покоящейся точки-причины (u_п = 0). Воспользовавшись формулами (3.11), (4.17) – (4.19), имеем

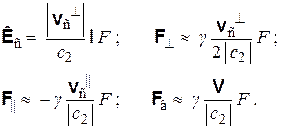(4.20)

Здесь учтено следующее: а) причинно-следственное звено, рассмотренное в разд. 3, представляет собой в действительности не само это звено, а пару одномоментных точек мировых линий причины и следствия, поэтому точки П, С и сила F_с из разд. 3 есть фактически точки П, С₀ (или П₀, С ) и сила F_кл из настоящего раздела (ср. рис. 3.1 – 3.3 с рис. 4.1, 4.2); б) формула (3.11), выписанная для случая u_п = 0, u_с^|| = 0, сохраняет силу и при u_с^|| ≠ 0, если заменить в ней величину v (равную |v_с|) на |v_с^┴| (так как согласно формулам (З.6) и (3.9) составляющая v_с^|| не дает вклада в силу К_с); в) u_с = v_с при u_п = 0. Отметим, что все четыре добавочные силы взаимно перпендикулярны (напомним, что орт l ортогонален векторам v_с и F_кл).

При взгляде на формулы (4.20) обращает на себя внимание их схожесть: все описываемые ими добавочные силы, во-первых, пропорциональны модулю «классической» силы, и, во-вторых, пропорциональны отношению соответствующей скорости к константе c₂. Данное обстоятельство служит еще одним, хотя, конечно, весьма косвенным, доводом в пользу введения добавочной силы К_с; во всяком случае, при отсутствии таковой была бы явно нарушена симметрия четырех линейно независимых направлений пространства-времени.

В завершение настоящего раздела обратим внимание на возможность дать две различные интерпретации фигуре, изображенной на рис. 4.1 (причем независимо от того, имеет сила F временню составляющую или нет). Одна интерпретация базируется на представлении о нашем Мире как трехмерной гиперплоскости со строго нулевой толщиной по оси времени. В соответствии с таким представлением рассматриваемая фигура есть изображение двух состояний Мира, разделенных интервалом времени 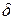t. При этом имеет место взаимодействие между будущим и прошлым состояниями Мира. Вторая интерпретация основывается на допущении, что наш Мир имеет некоторую ненулевую толщину по временной оси или, говоря в духе представлений квантовой механики, имеет «размазанность» или «неопределенность» вдоль этой оси. В этом случае можно сказать, что фигура на рис. 4.1 изображает две взаимодействующие материальные точки, принадлежащие одному и тому же состоянию Мира, но лежащие в разных его временных сечениях.