Допустим, что эти величины связаны между собой зависимостью, близкой к

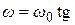
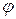(3.4)

где ω = |ω_x| = |ω| – модуль псевдовектора угловой скорости ω; ω₀ – константа размерности частоты. Тогда при 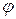= 0 имеем случай, изучаемый теоретической механикой, при этом система является чисто детерминированной. А при 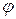= π/2 причинное воздействие полностью пропадает и система становится абсолютно индетерминированной (последнее вытекает из того, что при 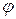= π/2 силы F_п и F_с направлены перпендикулярно прямой ПС и вращаются вокруг нее с бесконечно большой скоростью, из-за чего средние их значения по любому промежутку времени оказываются в точности равными нулю). Существование у системы двух таких предельных состояний – строго детерминированного и абсолютно недетерминированного – полностью согласуется с представлениями причинной механики.

Вариант 2. Пусть силы F_п и F_с отклоняются от прямой ПС следующим образом. Если скорость относительного движения причины П и следствия С направлена вдоль прямой ПС или равна нулю, то отклонение отсутствует. Если относительная скорость точек П и С направлена под углом к прямой ПС, то отклонение сил происходит в плоскости, которая перпендикулярна другой плоскости, проходящей через вектор относительной скорости и прямую ПС. При этом силы F_п и F_с, как ранее мы условились считать, отклоняются от прямой ПС в противоположные стороны и на одинаковый угол (рис. 3.3,а).

Рис. 3.3. Еще одно возможное воздействие времени на причинную связь: а – отклонение сил F_п и F_с от прямой ПС в плоскости β на угол 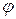, зависящий от скорости v_c; б – появление добавочных сил К_п и К_с, описываемых выражениями (3.6), (3.7) или (3.9), (3.10) (К_п = –К_с)

v_c – скорость движения точки-следствия С относительно точки-причины П; v_п – скорость точки П относительно точки С (v_п = –v_с); F_с1, F_с2, F_п1, F_п2 – составляющие сил действия F_с и противодействия F_п, направленные вдоль прямой ПС и перпендикулярно к ней; α – плоскость, проходящая через вектор относительной скорости v_c и прямую ПС; β – плоскость, перпендикулярная плоскости α и проходящая через прямую ПС; i_с, i_п – орты, лежащие на прямой ПС и направленные соответственно от точки П к точке С и от С к П (i_п = –i_с).

Конкретное из двух возможных направлений отклонения силы в указанной плоскости определим для каждого элемента причинно-следственного звена таким образом. Возьмем три вектора: вектор скорости, с которой рассматриваемый элемент движется относительно другого элемента; составляющую действующей на него силы, направленную вдоль прямой ПС; составляющую той же силы, направленную перпендикулярно прямой ПС. Пронумеруем эти векторы в перечисленном порядке.

Примем, что отклонение силы от прямой ПС происходит в такую сторону, при которой указанная упорядоченная тройка векторов образует для точки-причины левый, а для точки-следствия правый репер. Будем считать, что угол отклонения силы 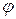зависит от скорости относительного движения причины и следствия, причем таким образом, что он стремится к нулю при сближении направлений вектора относительной скорости и прямой ПС.

Более детально данный вариант воздействия времени опишем для случая малого угла 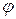. В этом случае отклонение сил от прямой ПС можно рассматривать, как результат действия на причину и следствие малых добавочных сил К_п и К_с, направленных перпендикулярно прямой ПС и связанных с углом 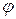соотношениями

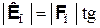
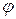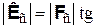
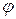; (3.5)

(рис. 3.3,б). Будем считать, что добавочные силы описываются выражениями

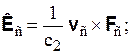(3.6)

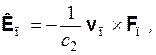(3.7)

где силы действия F_с и противодействия F_п направлены вдоль прямой ПС; v_с – скорость точки-следствия С относительно точки-причины П; v_п – скорость точки П относительно точки С (v_п = –v_с); c₂ – псевдоскалярный параметр размерности скорости, c₂ > 0 в правой системе координат (псевдоскалярность параметра c₂ нужна для компенсации псевдовекторногохарактера векторного произведения). Из F_п = –F_с, v_п = –v_с следует К_п = –К_с, как это и должно быть. В связи с тем, что мы рассматриваем случай 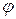<< 1, можно записать с учетом (3.5), (3.6):

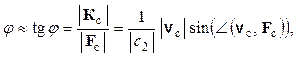(3.8)

поэтому должно выполняться условие |v_с|sin( 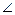(v_с, F_с)) << |c₂|. Для простоты будем предполагать, что |v_с| << |c₂|. Мы обсудим формулы (3.6), (3.7) ниже, после описания третьего возможного варианта воздействия времени на причинную связь.

Вариант 3. Допустим, что силы F_п и F_с отклоняются от прямой ПС таким же образом, как и в варианте 2, за одним исключением: направление отклонения определяется иной упорядоченной тройкой векторов. А именно, возьмем следующие три вектора: вектор относительной скорости рассматриваемого элемента причинно-следственного звена; единичный вектор, лежащий на прямой ПС и направленный от другого элемента в сторону данного; составляющую действующей на данный элемент силы, направленную перпендикулярно прямой ПС. (В варианте 2 вместо второго вектора бралась составляющая силы, направленная вдоль прямой ПС.) Примем, что отклонение силы от прямой ПС происходит в такую сторону, что эти три вектора, занумерованные в указанном порядке, образуют для точки-причины левый, а для точки-следствия правый репер. Угол отклонения силы 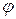пусть будет таким же, как в варианте 2.

Для малого угла 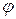опять можно заменить отклонение сил F_п и F_с от прямой ПС приложением к причине и следствию малых добавочных сил К_п и К_с, перпендикулярных прямой ПС и удовлетворяющих соотношениям (3.5). Будем считать, что эти силы описываются выражениями

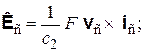(3.9)

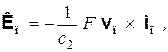(3.10)

где F = |F_с| = |F_п|; i_с, i_п — единичные векторы, лежащие на прямой ПС; i_с направлен от точки П к точке C, i_п направлен от точки С к точке П (i_п = –i_с); остальные обозначения те же, что и в формулах (3.6), (3.7) (см. рис. 3.3,6). Здесь, как и в варианте 2, полагаем выполненным условие |v_с| << |c₂|.

Рассмотрим один частный случай. Пусть в некоторой инерциальной системе координат точка-причина П покоится, а точка-следствие С равномерно обращается вокруг нее по окружности с центром в точке П. В этом случае относительная скорость v_с перпендикулярна к прямой ПС и направлена по касательной к окружности, поэтому формулы (3.9), (3.10) могут быть преобразованы к виду

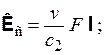(3.11)

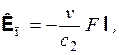(3.12)

где v = |v_с| = |v_п|; l – единичный псевдовектор, перпендикулярный векторам v_с и i_с и направленный в ту же сторону, что и псевдовектор v_с 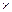i_с. Формулы (3.11), (3.12) согласуются с формулами для добавочных сил, приведенными в причинной механике [1]. Именно по аналогии с последними мы ввели для параметра, входящего в правые части наших формул, обозначение c₂. Отметим, что если взаимодействие причины и следствия имеет отталкивающий характер, то F_с = Fi_с, F_п = Fi_п, и тогда формулы (3.6), (3.7) из варианта 2 принимают вид (3.9), (3.10). Поэтому в описываемом частном случае они также могут быть представлены в форме (3.11), (3.12). Таким образом, предложенные варианты 2 и 3 воздействия времени на причинно-следственную связь можно рассматривать как возможные непосредственные обобщения соответствующих положений причинной механики.

Отметим, что различие между вариантами 2 и 3 наиболее заметно проявляется в случае знакопеременного взаимодействия между причиной и следствием: при изменении знаков сил F_с и F_п добавочные силы К_с и К_п в варианте 2 тоже меняют знаки, а в варианте 3 остаются без изменений. Отметим также, что, строго говоря, появление добавочных сил определенной величины и отклонение «классических» сил на угол, определяемый зависимостями (3.5), представляют собой не тождественные результаты. Однако при добавочных силах, существенно меньших (по модулю) «классических» сил, эти результаты различаются на малую второго порядка по углу отклонения, и при достигнутой в экспериментах Н. А. Козырева точности измерений они не различимы.

Существенным свойством добавочных сил К_с и К_п, введенных в вариантах 2 и 3, является то, что они не производят в сумме работы над причинно-следственным звеном.

В самом деле, суммарное приращение работы этих сил ∆A за малый промежуток времени ∆t составляет

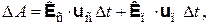(3.13)

где u_с, u_п – скорости следствия и причины относительно рассматриваемой инерциальной системы координат. Учитывая, что К_п = –К_с и что следствие движется относительно причины со скоростью v_с = u_с – u_п, находим из равенства (3.13):

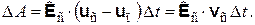
А так как согласно формулам (3.6), (3.9) добавочная сила К_с перпендикулярна вектору скорости v_с, то отсюда и получаем, что ΔA = 0.

Данный результат имеет принципиальное значение. Он означает, что для осуществления воздействия на причинно-следственное звено, описываемое вариантами 2 и 3, не требуется производить дополнительных затрат работы. Не изменяется при таком воздействии и энергия системы. Отметим также, что из равенства нулю главного вектора добавочных сил (К_с + К_п = 0) следует неизменность суммарного импульса системы. Вместе с тем, рассматри­ваемое воздействие может изменять момент количества движения системы и траектории элементов, составляющих причинно-следственное звено. Возможно, что именно к такому варианту воздействия времени на причинную связь склонялся по мере развития своих представлений Н. А. Козырев. Если в первых публикациях по причинной механике ученый пишет о том, что время может пополнять энергию системы, то в более поздних работах он утверждает, что время через свои физические свойства повышает организованность вещества, препятствуя (в какой-то степени) возрастанию энтропии в системе, то есть время является источником негэнтропии в нашем Мире.

Итак, мы рассмотрели три возможных варианта отклонения векторов сил от прямой ПС, соединяющей взаимодействующие точки. В рамках классической механики такое отклонение не может быть объяснено свойствами самого причинно-следственного звена. Дело в том, что в классической механике материальные точки не наделяются внутренней структурой, поэтому их симметрия совпадает с симметрией геометрической точки. Из этого следует, что среди элементов симметрии причинно-следственного звена имеются ось вращения бесконечного порядка, проходящая через обе образующие его точки, и плоскости зеркальной симметрии, содержащие прямую ПС. При наличии таких элементов симметрии внутренние причины не способны привести к отклонению силы взаимодействия от прямой ПС в каком-либо определенном направлении (как это имеет место в вариантах 2 и 3) или же к ее отклонению и вращению в какую-нибудь определенную сторону (как в варианте 1). Поэтому с позиции классической механики рассматриваемое отклонение может быть вызвано только причиной, внешней по отношению к причинно-следственному звену.

Три рассмотренные варианта воздействия времени на причинную связь, разумеется, не единственно возможные. Однако определить, какой из этих или других возможных вариантов верно отражает реальную действительность, можно только на основании специальных опытов.

Из содержания настоящего раздела видно, что принципиальная возможность отклонения сил от прямой, соединяющей взаимодействующие точки, фактически содержится уже в самй классической механике (в ней не имеется только физической причины, которая обусловила бы отклонение сил в определенном направлении). Поэтому причинную механику Козырева можно рассматривать как естественное развитие классической механики Ньютона.