О характеристике времени с2 в теории Н. А. Козырева

Эксперимент по измерению хода времени с₂ проводился Н. А. Козыревым путем взвешивания вращающегося гироскопа с вертикально ориентированной осью [1]. При введении в систему весы–гироскоп вертикальных вибраций наблюдалось изменение веса гироскопа на величину ∆Ф, пропорциональную его весу Ф и линейной скорости вращения ротора v; значение параметра с₂ вычислялось из формулы

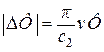(2.1)

и оказалось приблизительно равным 2200 км/с [1, с. 366 – 367, 382]. Н. А. Козырев трактовал данный факт как появление в системе добавочных сил, не учитываемых классической механикой. Ученый постулировал, что с₂ есть псевдоскаляр, так как при замене исследуемой физической системы на зеркально симметричную эффект менял знак.

Ход времени с₂ определяется в причинной механике как скорость реализации причинного воздействия в элементарном причинно-следственном звене, состоящем из двух материальных точек — точки-причины и точки-следствия:

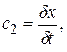(2.2)

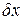где и 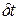– сколь угодно малые, но не равные нулю пространственное и временне различия между точкой-причиной и точкой-следствием.

Данное определение придает важнейшей в причинной механике характеристике времени ясный физический смысл. Оправданность введения именно такого определения подкрепляется результатами предыдущего раздела, в котором доказано, что величина с₂ есть фундаментальная константа. Однако приведенное определение все же обладает рядом недостатков.

1. Ход времени с₂ определяется равенством (2.2) через величины 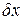и 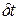, не поддающиеся непосредственному экспериментальному измерению.

2. Равенство (2.2) не отвечает псевдоскалярному характеру с₂ (принимаемое Н. А. Козыревым допущение о псевдоскалярности временного интервала 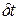не достаточно веско аргументировано в [1], и поэтому оно пока что не может считаться оправданным).

3. Рассматриваемое определение приводит к несогласованности между проявляющейся в астрономических наблюдениях [6, 7] мгновенности передачи воздействия через время на космические расстояния и конечностью скорости передачи такого воздействия в элементарном причинно-следственном звене.

4. В [1] не проведено строго логического перехода от определения (2.2) к формуле для добавочных сил (2.1) (такой переход, скорее всего, в принципе невозможен, так как, располагая единственной скалярной величиной с₂, нельзя сделать однозначного заключения о значении векторной величины, каковой является добавочная сила), поэтому фигурирующая в формуле (2.1) величина с₂, вообще говоря, не обязана совпадать с величиной, определяемой равенством (2.2).

В связи с тем, что приведенное определение имеет указанные недостатки, представляется целесообразным дать иное определение хода времени, которое сохраняло бы наиболее существенные черты величины с₂, описанные в [1], но было бы лишено отмеченных недостатков. Такое определение предлагается ниже.

В соответствии с положениями причинной механики будем считать, что время посредством своих активных свойств по-разному взаимодействует с правыми и левыми физическими системами. Одним из простейших математических объектов, различающих правое и левое, является пара (а, ω) коллинеарных между собой вектора a и псевдовектора ω (рис. 2.1). (Простой пример: движение в направлении, указываемом вектором a, с одновременным вращением в сторону, определяемую псевдовектором ω, является правовинтовым при совпадении направлений а и ω и левовинтовым, когда направления а и ω взаимно противоположны.) Допустим, что ход времени описывается именно таким математическим объектом. Тогда он, очевидно, может проявляться в физических системах, кинематика которых характеризуется аналогичной парой векторов. Как раз такой случай реализован в описанном выше опыте с вибрирующим гироскопом, где такую кинематическую пару образуют вызываемое вибрацией ускорение гироскопа а = аk и угловая скорость его вращения ω= ωk (здесь а – скаляр, ω – псевдоскаляр, k – направляющий орт оси вращения).

Рис. 2.1. Пара коллинеарных вектора а и псевдовектора ω

Показанное направление псевдовектора ωсоответствует в правой системе координат отмеченному направлению обхода окружности.

Можно предположить, что воздействие физических свойств времени на гироскоп приводит к появлению добавок ∆а и ∆ω к величинам а и ω, которые являются монотонными функциями этих величин, удовлетворяют условию ∆а = ∆ω = 0 при aω = 0 и имеют знаки, зависящие от взаимной ориентации векторов а и ω. Тогда в линейном по а и ω приближении можем записать:

(2.3)

где k_a и k_ω – некоторые размерные коэффициенты; знаки выражений положительны при одной взаимной ориентации векторов a, ω и отрицательны при другой их взаимной ориентации.

При вибрировании гироскопа ускорение a периодически меняет знак, а угловая скорость ω остается неизменной. При этом среднее по времени значение добавки ∆а оказывается отличным от нуля, несмотря на равенство нулю среднего значения ускорения а. Это связано с тем, что знак ∆а одинаков на любом полупериоде вибрации в силу зависимости его как от знака а, так и от взаимной ориентации а и ω, изменяющейся вместе с изменением знака а. Умножая среднее значение ∆а на массу ротора гироскопа, получаем среднее значение добавочной силы, действующей на гироскоп:

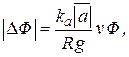(2.4)

здесь использовано соотношение 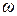= v/R, кроме того, масса ротора приравнена к массе всего гироскопа 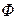/g, как это сделано в [1]; R и v – некоторые средние значения радиуса ротора и линейной скорости его вращения; 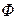– вес гироскопа; g – ускорение свободного падения; черта над символом – операция усреднения по времени. Мы не уточняем знак величины ∆ 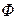, так как он всегда может быть согласован с наблюдаемым посредством выбора нужного знака в (2.3). Величина ∆ 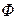, очевидно, может быть интерпретирована как изменение веса гироскопа.

Сравним выражение (2.4) с полученным экспериментальным путем соотношением (2.1). Видно, что выражение (2.4) включает в себя ту же, что и соотношение (2.1), зависимость добавочной силы от линейной скорости вращения ротора v и от веса гироскопа 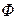. Это дает основание сделать вывод о справедливости первого из равенств (2.3), поскольку именно на нем базируется выражение (2.4). Подчеркнем, что различие множителей при v 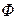в формулах (2.1) и (2.4) не служит аргументом против данного вывода. Дело в том, что соотношение (2.1), будучи выражением лишь частных опытных данных, носит ограниченный характер. В нем, в частности, не отражена зависимость добавочной силы от интенсивности вибраций и геометрических параметров гироскопа, которая, очевидно, должна иметь место в реальности и которая как раз и учитывается упомянутым множителем в формуле (2.4).

Итак, мы подтвердили справедливость первого из равенств (2.3). Ясно, что коэффициент k_a, входящий в это равенство, может зависеть от характеристик вибрации и размеров гироскопа. Допустим, что второе равенство в (2.3) тоже верно и коэффициент k_ω в нем зависит от свойств системы в точности так, как и коэффициент k_a (в [1] измерения ∆ω не проводились, поэтому мы не можем сопоставить это допущение с опытными данными). Тогда отношение ∆a/∆ω представляет собой псевдоскаляр, имеющий размерность скорости и не зависящий от конкретных свойств изучаемой физической системы.

Величину ∆a/∆ω естественно и принять в качестве хода времени c₂. Легко убедиться в том, что определяемая таким образом величина c₂ лишена отмеченных ранее недостатков, которые свойственны определению ее, базирующемуся на равенстве (2.2).

Предложенный подход к определению хода времени допускает распространение на физические системы, не связанные с вращающимися телами. Для таких систем роль пары (a, ω) в определении c₂ будут играть другие величины, например, плотность потока энергии и плотность объемных моментов сил.

Примечание. Содержание настоящего раздела было изложено в виде рукописной заметки в апреле 1979 года и тогда же обсуждено с Н. А. Козыревым. Им были сделаны следующие два замечания.

1. В схеме, изображенной на рис. 2.1, в случае, когда a — ускорение, на систему действует нескомпенсированная сила, что ведет к нарушению закона сохранения импульса. Между тем, справедливость этого закона была проверена с большой точностью в специальных опытах, когда и источник вибрации, и гироскоп помещались на одну чашу весов. В таких опытах добавочные силы не регистрировались.

2. Формула (2.4) содержит радиус ротора R. Чтобы привести ее к виду (2.1), нужно принять, что k_a ~ R. Но в этом случае не ясен физический смысл формулы (2.3). Опыты с гироскопами, у которых ротор имел форму тонкостенного стакана (так что с хорошей точностью выполнялось условие R = const), а также анализ асимметрии фигур планет и исследование широтной зависимости эффекта изменения веса гироскопа убеждают в том, что в формуле (2.4) должно стоять не отношение v/R = 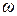, а именно линейная скорость точек ротора v.

Рис. 2.2. Возможная система векторов для двух

взаимодействующих объектов

Ответом на первое замечание Н. А. Козырева служит рис. 2.2, на котором изображена возможная система векторов для причинно-следственного звена в целом. Видно, что в такой системе отсутствуют нескомпенсированные силы, и закон сохранения импульса выполняется. Ответа на второе замечание автор не имеет.