Чувствительность систем автоматического управления

Чувствительность систем автоматического управления - это степень влияния разброса параметров и их изменений в процессе работы на статические и динамические свойства системы управления, то есть на точность, показатели качества, на частотные свойства и др.

Параметры системы управления (коэффициенты передачи и постоянные времени) определяются физическими параметрами составляющих ее элементов (резисторов, конденсаторов, катушек индуктивностей и т.п.). Величины физических параметров элементов, во-первых, имеют технологический разброс, обусловленный допусками на изготовление элементов, во-вторых, подвержены эксплуатационным изменениям с течением времени, что обусловлено их старением.

Поэтому встает задача оценки работы системы при изменении и разбросе параметров составляющих ее элементов.

Эта задача решается путем количественной оценки чувствительности системы. Для этого требуется описать систему управления уравнениями в нормальной форме [2], т.е.

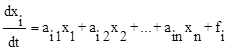при i=1, 2, ... , n, (7.13)

где n - порядок системы;

x_i - координаты состояния системы;

f_i - внешние воздействия, прикладываемое к системе;

a_ik - коэффициенты уравнения, определяемые величинами физических параметров составляющих систему элементов.

Изменяющиеся со временем параметры элементов системы в процессе эксплуатации и от разброса при изготовлении обозначим через a_j (j=1, 2, ... , m).

Тогда уравнение системы (7.13) можно записать в виде

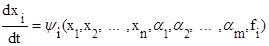при i=1, 2, ... , n. (7.14)

Решение уравнений (7.14) определяет координаты системы: x₁(t), x₂(t), ... , x_n(t), образующие исходное движение системы.

Пусть параметры a_j изменяются на малые величины Da_j , тогда имеем

;

. . . . . . . . . .

.

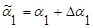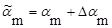Рассматривая малые изменения параметров a_j (j=1, 2, ... , m), получим новые уравнения

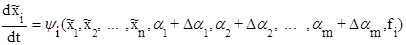(7.15)

при i=1, 2, ... , n.

Процесс в той же системе, но с измененными параметрами, определяемый решением уравнений (7.15), т.е. 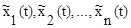, называется варьированным движением.

Возникшее различие в протекании процессов в системе за счет изменения параметров

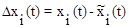при i=1, 2, ... , n

называется дополнительным движением.

При малых отклонениях Da_j эта разность может быть определена следующим образом:

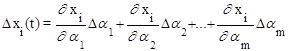при i=1, 2, ... , n. (7.16)

Обозначим

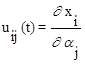(j=1, 2, ... , m). (7.17)

Тогда дополнительное движение будет

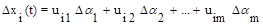при i=1, 2, ... , n. (7.18)

Величины 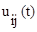, определяемые выражением (7.17), представляют собой функции чувствительности i-ой координаты системы по j-ому параметру.

Таким образом, чтобы оценить степень влияния разброса и изменения параметров на координаты системы необходимо определить функции чувствительности по каждой координате от каждого изменяющегося параметра.

В рассматриваемом случае x_i(t) являются координатами состояния системы. Вообще же аналогичные характеристики чувствительности вводятся так же для различных показателей качества системы. Тогда в формуле (7.17) вместо x_i будет стоять соответствующий показатель качества, а в формуле (7.18) - вместо Dx_i - изменение этого показателя качества. Функции чувствительности для частотных характеристик будут функциями не времени, а частоты. Если показатели качества выражаются не функциями, а числами, то u_ij называются коэффициентами чувствительности.

Если в качестве изменяющихся параметров a_j выбрать внешние воздействия, то можно получить функции чувствительности системы по отношению к внешним воздействиям.

Определение функций чувствительности производится следующим образом.

Продифференцируем исходное уравнение (7.14) по изменяющимся параметрам a_j. Тогда получим

.

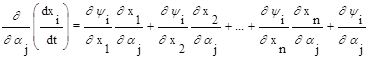Меняя в левой части порядок дифференцирования и учитывая (7.17), получим выражения

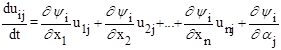при i=1,...,n; j=1,...,m; (7.19)

которые называются уравнениями чувствительности. Решение этих уравнений определяет функции чувствительности .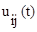

Рассмотрим функции чувствительности для частотных характеристик. Передаточную функцию разомкнутой системы запишем в виде

W(s) = W(s, a₁, a₂, ... , a_m ), (7.20)

где a₁, a₂, ... , a_m - параметры системы, имеющие технологический разброс или эксплуатационные изменения.

Тогда амплитудная и фазовая частотные характеристики тоже зависят от этих параметров

А(w) = А(w, a₁, ... , a_m);

y(w) = y(w, a₁, ... , a_m).

Функции чувствительности для амплитудной и фазовой частотных характеристик будут

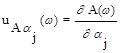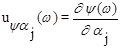, , j=1, 2, ... , m. (7.21)

В результате получим как функции частоты выражения для отклонения частотных характеристик за счет разброса и изменения параметров системы:

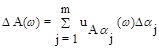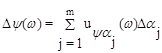, . (7.22)

Определение функций чувствительности производится при проектировании систем с наименьшими изменениями качественных показателей при отклонении значений параметров системы от расчетных.

Пример. Определить функции чувствительности для системы, заданной следующим уравнением (Tp+1)x(t)=kg(t), где T, k - изменяющиеся параметры.

Решение. Уравнение системы в нормальной форме имеет вид

.

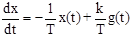Введем функции чувствительности

, .

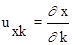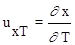Уравнение чувствительности получим исходя из (7.19)

;

.

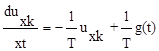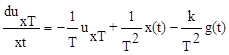Найдя отсюда u_xk и u_xT, вычислим изменение хода процесса управляемой величины x(t) за счет изменения параметров k и T по формуле

.

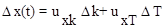Передаточная функция системы: .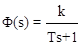

Частотные характеристики: , .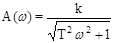

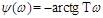Найдем функции чувствительности частотных характеристик по параметру T

= ,

= .

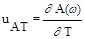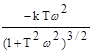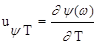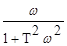Отклонения частотных характеристик

DA(w) = u_AT(w)DT, Dy(w) = u_YT(w)DT.

ВОПРОСЫ К РАЗДЕЛУ 7

1. Перечислите общие методы повышения точности систем управления. Поясните их.

2. Дайте понятие астатических системы управления. Каким образом определяется степень астатизма?

3. В чем преимущество повышения степени астатизма системы с помощью изодромных устройств?

4. Какая система является инвариантной по отношению к внешним воздействиям?

5. Что понимается под комбинированным управлением?

6. Как определяются передаточные функции компенсирующих устройств в комбинированных системах?

7. Для каких целей используются неединичные главные обратные связи?

8. Сформулируйте понятие чувствительности систем управления.

9. Каким образом можно получить уравнения чувствительности?

10.Что представляют собой функции чувствительности и коэффициенты чувствительности?

Содержание Глоссарий