Частотные критерии устойчивости
Частотные критерии устойчивости базируются на принципе аргумента. Рассмотрим этот принцип, для чего запишем выражение для характеристического вектора, которое получим из характеристического полинома системы (4.2), предварительно разложенного на множители, путем замены p на jw:
D(jw) = an(jw- p1)(jw- p2)...(jw- pn), (5.9)
где pi - корни характеристического уравнения (полюсы системы).
Определим изменение аргумента вектора D(jw) при изменении частоты w от -¥ до +¥
D arg D(jw) =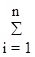 
arg(jw- pi) при -¥ £w£+¥.
Если корень характеристического уравнения pi расположен на комплексной плоскости слева от мнимой оси, то вектор (jw-pi) поворачивается на угол p, если этот корень находится на комплексной плоскости справа от мнимой оси, то вектор (jw-pi) поворачивается на угол -p. Допустим, что m корней характеристического уравнения расположены справа от мнимой оси, а остальные n-m корней - слева. Тогда изменение аргумента характеристического вектора равно
D arg D(jw) = (n-m)p при -¥ £w£+¥.
В устойчивой системе m=0, и изменение аргумента характеристического вектора получается следующим:
D arg D(jw) = n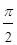 
при 0£w£+¥. (5.10)
Дата добавления: 2015-06-01; просмотров: 863;