Критерий Рауса.

Линейная система, характеристический полином которой равен

,

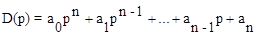где a₀>0, устойчива, если положительны все элементы первого столбца следующей таблицы

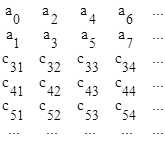(5.7)

В первой строке таблицы Рауса расположены четные коэффициенты характеристического полинома, во второй - нечетные. Если степень характеристического полинома - четное число, то последний элемент второй строки равен нулю. Третья и последующие строки определяются следующим образом:

с_ij = с_i-1,1´с_i-2,j+1 - с_i-2,1´с_i-1,j+1; с_i,L = 0 ;

i = 3, 4, ... , n+1; j = 1, 2, ... , L-1; L = [0.5´n]+1.

Знак [ ] означает целую часть числа.