Дифференциальные уравнения и передаточные функции замкнутых систем управления
Система автоматического управления представляет собой совокупность объекта управления, регулятора и датчика рассогласования. Обобщенная функциональная схема системы управления представлена на рис.4.1.
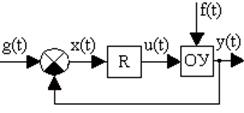
Рис. 4.1. Функциональная схема системы управления
Для того, чтобы получить математическое описание системы управления, необходимо составить по рассмотренной ранее методике линеаризованные уравнения всех элементов, из которых состоит датчик рассогласования, регулятор и объект управления. Таким образом получим систему дифференциальных уравнений, описывающую исследуемую систему управления. Полученная система дифференциальных уравнений путем исключения промежуточных переменных может быть разрешена относительно любой координаты системы управления. Обычно она решается либо относительно рассогласования x(t), т.е. ошибки, либо относительно управляемой величины y(t).
Первый случай встречается чаще, так как исследование изменения ошибки, как правило, является более важным. В этом случае получается дифференциальное уравнение
D(p)x(t) = Q(p)g(t) + N(p)f(t). (4.1)
Полином D(p) степени n от символа дифференцирования p характеризует свободное движение системы. Он называется характеристическим полиномоми может быть представлен в виде
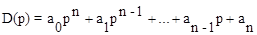 , (4.2)
, (4.2)
где a0,...,an в линеаризованной системе представляют собой постоянные коэффициенты.
Полином Q(p) степени m (m£n) от символа дифференцирования p определяет влияние задающего воздействия g(t) на характер изменения ошибки.
Полином N(p) степени k (k£n) от символа дифференцирования p определяет влияние возмущающего воздействия f(t) на характер изменения ошибки. В принципе таких возмущений может быть несколько. Однако вследствие линейности действует принцип суперпозиции и достаточно рассмотреть методику учета только одного воздействия; при наличии нескольких возмущений необходимо лишь просуммировать результат.
Из (4.1) вытекает, что ошибка может быть представлена в виде суммы двух составляющих: первая составляющая определяется влиянием задающего воздействия, вторая - возмущающего воздействия.
При решении системы дифференциальных уравнений относительно управляемой величины получается уравнение движения объекта управления при наличии регулятора. Это уравнение получается в результате подстановки выражения для ошибки x(t)=g(t)-y(t) в уравнение (4.1):
D(p)y(t) = R(p)g(t) - N(p)f(t), (4.3)
где
R(p) = D(p) - Q(p).
Полином R(p) определяет влияние задающего воздействия g(t) на управляемую величину.
Уравнения (4.1) и (4.3) являются исходными дифференциальными уравнениями замкнутой системы управления. При известных функциях времени в правых частях уравнений (4.1) и (4.3) они могут быть решены относительно искомых функций времени, т.е. может быть найдено изменение ошибки управления во времени и движение объекта управления.
Таким образом, четверка полиномов D(p), Q(p), N(p), R(p) полностью определяет замкнутую систему управления.
Уравнения, описывающие динамику системы, также как и звена, могут быть представлены в другой форме. Для этого перепишем уравнения (4.1) и (4.3) в операторном виде, перейдя от функций времени к их изображениям по Лапласу.
В результате получим:
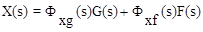 , (4.4)
, (4.4)
где 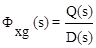 ;
; 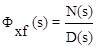 .
.
При f(t)=0 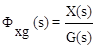 - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
- передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
При g(t)=0 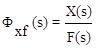 - передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.
- передаточная функция замкнутой системы по ошибке относительно возмущающего воздействия.
Аналогично:
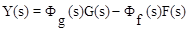 , (4.5)
, (4.5)
где 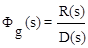 ;
; 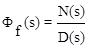 .
.
При f(t)=0 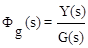 - передаточная функция замкнутой системы по задающему воздействию, главный оператор системы Ф(s).
- передаточная функция замкнутой системы по задающему воздействию, главный оператор системы Ф(s).
При g(t)=0 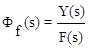 - передаточная функция замкнутой системы по возмущающему воздействию.
- передаточная функция замкнутой системы по возмущающему воздействию.
Сравнивая уравнения (4.4) и (4.5) видно, что |Фf(s)| = |Фxf(s)|.
Таким образом, четверка передаточных функций Фg(s), Фf(s), Фxg(s), Фxf(s) полностью определяет замкнутую систему управления.
Выразим передаточные функции замкнутой системы через передаточные функции ее отдельных элементов. Для этого на основании функциональной схемы системы (рис.4.1) и уравнения (4.3) изобразим структурную схему системы (рис.4.2).
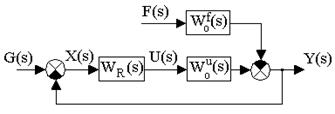
Рис. 4.2. Структурная схема системы управления
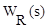 - передаточная функция регулятора;
- передаточная функция регулятора;
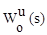 - передаточная функция объекта управления по управляющему воздействию;
- передаточная функция объекта управления по управляющему воздействию;
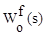 - передаточная функция объекта управления по возмущающему воздействию;
- передаточная функция объекта управления по возмущающему воздействию;
G(s), F(s), U(s), X(s), Y(s) - изображения по Лапласу задающего, возмущающего и управляющего воздействий, рассогласования и управляемой величины.
Если в системе ликвидировать обратную связь, то система из замкнутой превратится в разомкнутую. Звенья, расположенные между выходом сравнивающего устройства и его инверсным входом, образуют разомкнутую систему, передаточная функция которой имеет вид:
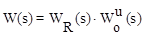 . (4.6)
. (4.6)
Передаточная функция разомкнутой системы W(s) имеет большое значение в классической теории управления, так как методы анализа и синтеза систем основаны на ее использовании.
Найдем передаточные функции замкнутой системы.
1. По задающему воздействию при f(t)=0. В этом случае исходная структурная схема системы (рис.4.2) может быть приведена к виду, изображенному на рис. 4.3.
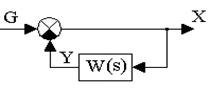
Рис. 4.3. Приведенная структурная схема системы управления
По определению 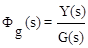 ;
; 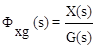 , тогда из рис.4.3 следует:
, тогда из рис.4.3 следует:
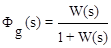 ;
; 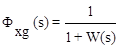 . (4.7)
. (4.7)
2. По возмущающему воздействию при g(t)=0. В этом случае исходная структурная схема системы (рис.4.2) может быть приведена к виду, изображенному на рис. 4.4.
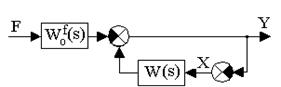
Рис. 4.4. Приведенная структурная схема
По определению 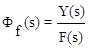 ;
; 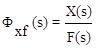 , тогда из рис.4.4 следует:
, тогда из рис.4.4 следует:
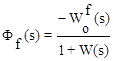 ;
; 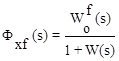 . (4.8)
. (4.8)
Таким образом, передаточные функции замкнутой системы определяются передаточной функцией разомкнутой системы.
Важные соотношения, вытекающие из вышеприведенного:
1. 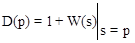 ;
;
2. 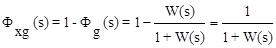 ;
;
3. 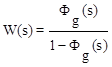 ; 4.
; 4. 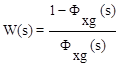 .
.
Пример. Определить передаточные функции системы, структурная схема которой имеет вид, представленный на рис. 4.5.

Рис. 4.5. Структурная схема системы управления
Решение:Запишем передаточную функцию разомкнутой системы:
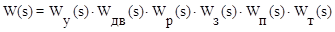 ,
,
тогда передаточные функции замкнутой системы будут:
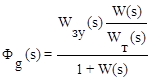 ;
; 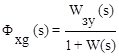 .
.
Дата добавления: 2015-06-01; просмотров: 1298;
