Неминимально-фазовые звенья

Неминимально-фазовые звенья - это такие звенья, которые, в отличие от обычных типовых звеньев, при равенстве амплитудных частотных характеристик имеют большие по абсолютному значению фазовые сдвиги. Одной амплитудной частотной характеристике неминимально-фазовых звеньев может соответствовать несколько различных фазовых частотных характеристик.

Звено с чистым запаздыванием.Это такое звено, у которого выходная величина повторяет входную с некоторой задержкой во времени. Уравнение и передаточная функция звена:

y(t) = x(t-t), 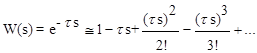, (3.44)

где t - время чистого запаздывания.

Амплитудно-фазовая частотная характеристика:

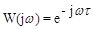, А(w) = 1, y(w)= -tw [рад]= 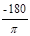tw [угл.град]. (3.45)

Переходная и весовая функции:

h(t) = 1(t-t), w(t) = d(t-t). (3.46)

Разница между этим звеном и безынерционным, как видим, в величине фазы. Амплитудные же характеристики одинаковы.

Примерами таких звеньев могут служить линия связи, трубопро-вод, транспортер, конвейер и др.

Звено с положительным полюсом.Передаточная функция звена имеет вид 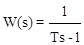. (3.47)

Здесь имеется положительный полюс ( корень знаменателя) s₁=1/T. В полюсе передаточная функция стремится к бесконечности (W(s)®¥). Амплитудно-фазовая частотная характеристика:

W(jw) = 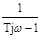, , 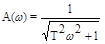y(w) = -p + arctg wT. (3.48)

Разница между этим звеном и апериодическим первого порядка, как видим, в величине фазы. Амплитудные же характеристики одинаковы.

Звено с положительным нулем.Передаточная функция звена имеет вид

W(s) = (1- ts) . (3.49)

Здесь имеется положительный нуль (корень числителя) s₁=1/t. В нуле передаточная функция равна нулю (W(s)=0).

Амплитудно-фазовая частотная характеристика:

W(jw) = (1 - jwt ), A(w)= 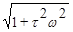, y(w) = - arctg wt. (3.50)

Разница между этим звеном и форсирующим первого порядка только в величине фазы. Амплитудные же характеристики одинаковы.