Интегрирующие звенья

1) Идеальное интегрирующее звено.

Уравнение движения звена - dx_вых/dt=K·x_вх;

В операторной форме - S·X_вых(S)=K·X_вх(S);

Передаточная функция - W(S)=K/S

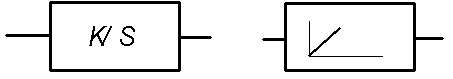
пример звена: редуктор, на входе которого – частота вращения; на выходе – угол поворота.

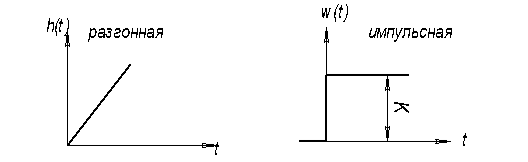
Частотная передаточная функция

W(iω)=K/iω=0-i·K/ω;

A(ω)=K/ω; φ(ω)=arctg(-K/ω·0)=-π/2 - фазовый сдвиг;

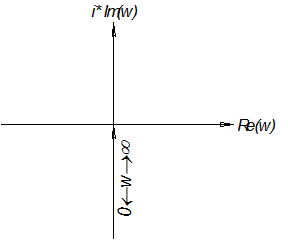
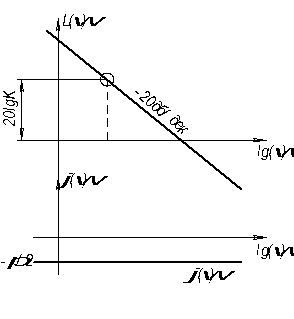
L(ω)=20·lgA(ω)=20·lg(K/ω)=20·lgK-20·lgω;

L(1)=20·lgK;

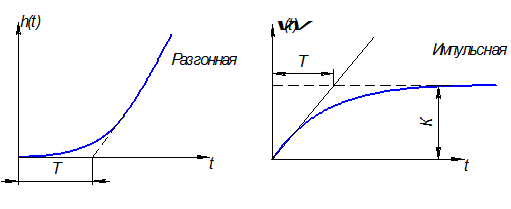
2) Реальное интегрирующее звено.

Уравнение движения в дифференциальной форме - d²x_вых/dt² + dx_вых/dt = K·x_вх;

В операторной форме - S²·X_вых(S)+S·X_вых(S)=K·X_вх(S);

Передаточная функция - W(S)=K/(S·(T·S+1))

Пример звена: электродвигатель, обладающий инерционностью подвижных элементов.

T_M=Ј·Ω_xx/M_П; Эл. двигатель, у которого на выходе надо получить угол поворота.

W(i·ω)=K/(i·ω·(T·i·ω+1))=-K·T/(1+T²·ω²)-i·K/(ω·(1+T²·ω²))

A(ω)=K/(ω·(1+T²·ω²)^1/2); φ=-π+arctg(1/T·ω);

A(0)→∞; A(∞)→0; φ(0)=-π/2; φ(∞)=-π;

L(ω)=20·lgA(ω)=20·lgK-20·lgω-20·lg(1+T²·ω²)^1/2

Общие свойства интегрирующих звеньев:

1) скорость изменения выходного сигнала пропорциональна величине входного сигнала;

2) все звенья вносят фазовые отставания;

3) сигнал на выходе звена может присутствовать даже при отсутствии сигнала на входе;

4) звенья плохо пропускают сигналы высокой частоты.