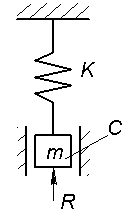
Механический колебательный контур

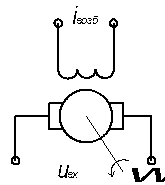
Электродвигатель, у которого нельзя пренебречь индуктивностью якоря.

Т_М=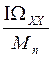

Т_Я=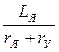

Уравнение движения этого электродвигателя двигателя

(Т_Я·Т_М·S²+T_МS+1)·Ω(S)=К·U_BХ(S)

Если для этого случая выполняется условие

Т_М>2Т_Я·Т_М, то Т_2,3= 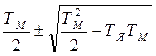- апериодическое звено 2-го порядка
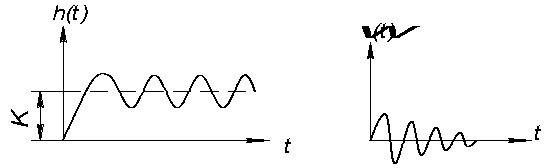
1) ξ=0 – консервативное: W(S)= 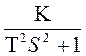колебания будут незатухающие – звено будет колебаться с частотой w0, чем объясняется название собственная частота.

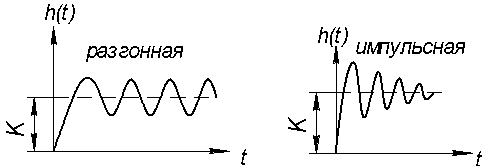
W(iω)= 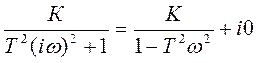, где - действительная, i0 - мнимая

ω → 0 Re=K ω → ∞ Re=0 ω =1/Т

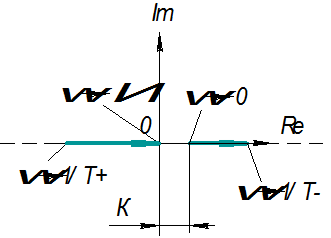
Если ω < 1/Т; φ(ω)=0. Если ω >1/Т; φ(ω)= -π

2) собственно колебательное 0<ξ≤1

W(S)=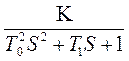

W(S)=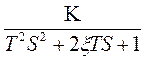

W(iω)= =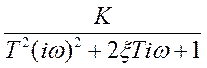

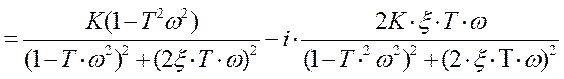
A(ω)= =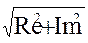

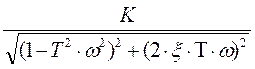
tgφ(ω)= ˉ 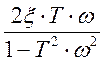- фазовый сдвиг в 4 четверти

φ(ω)= -π +arctg 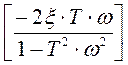- фазовый сдвиг в 3 четверти

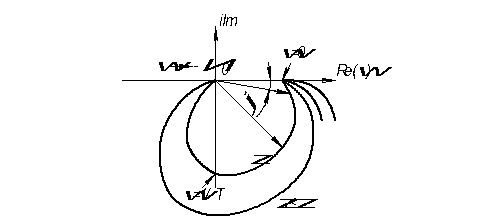
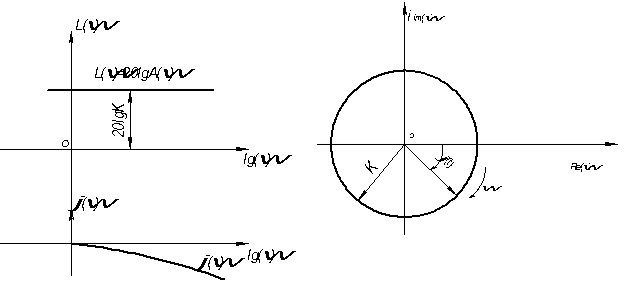
3) ξ>1

W(S) =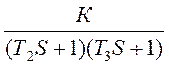

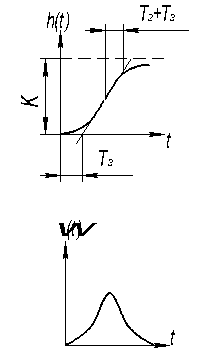
W(iω)=

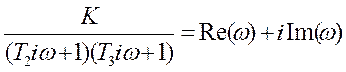
A(ω)=

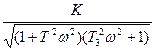
φ(ω)=-arctg (T₂ω)-arctg (T₃ω)

Логарифмическая частотная характеристика

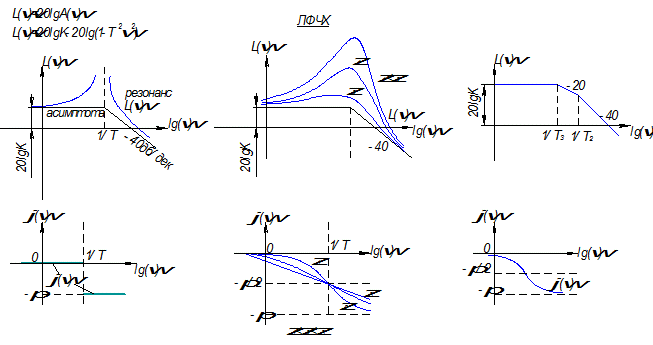
4. Запаздывающее звено

Х_ВЫХ(t)=КХ_ВХ(t-τ)

Разложим Х_ВХ(t-τ) в ряд

Х_ВХ(t-τ)=Х_ВХ+ +...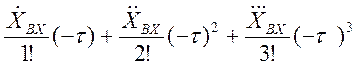

Х_ВХ(t-τ)→(1+ 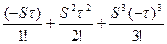+...)Х_ВХ(S)

(1+ 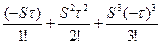+...)=e^Sτ

W(S) = Ke^-Sτ – время чистого запаздывания

Примеры реализации: длинные трубопроводы, нагревательные элементы, изменение силового режима при резании при резком изменении глубины резания

Поведение звена в переходных характеристиках:

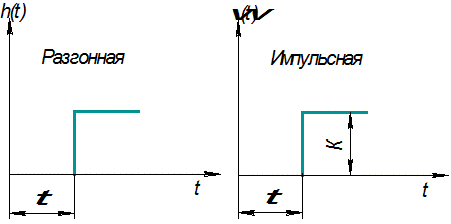
W(iω)=Ke^-iωτ=K(cos(ωτ)-i sin(ωτ))

A(ω)=K

tgφ= - 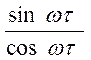= -tg(ωτ); φ(ω)=-ωτ

Общие свойства позиционных звеньев:

1. По окончании режима выходной сигнал прямопропорционален входному.

2. Если сигнал на входе в установившемся режиме отсутствует (=0), то по окончании процесса выходной сигнал так же =0.

3. Все звенья вносят отрицательные фазовые сдвиги, т.е. создают фазовые отставания выходного сигнала. ИСКЛЮЧЕНИЕ - БЕЗИНЕРЦИОННОЕ ЗВЕНО.

4. Звенья плохо пропускают высокочастотные колебания, т.к. при частоте стремящейся к бесконечности А→0, ИСКЛЮЧЕНИЕ - БЕЗИНЕРЦИОННОЕ ЗВЕНО.