Магнитное поле соленоида и тороида.

Можно рассчитать, применяя теорему о циркуляции, индукцию магнитно­го поля внутри соленоида. Рассмотрим соленоид длиной lимеющий N витков, по которому течет ток (рис.3.10.1).

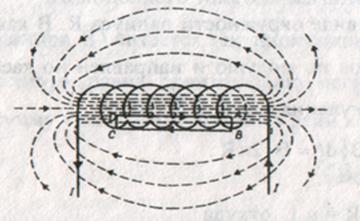Длину соленоида считаем во много раз больше, чем диаметр его витков, т.е. рас­сматриваемый соленоид бесконечно длинный. Внутри соленоида поле являет­ся однородным, вне соленоида - неодно­родным и очень слабым.

Из расчетов приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

Рис.3.10.1

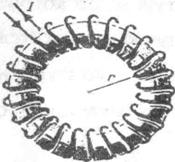
Важное значение для практики имеет также магнитное поле тороида -кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора(рис.3.10.2).

Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне него поле отсутствует. Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены, но оси тороида. В качест­ве контура выберем одну такую окружность радиуса г.

Рис.3.10.2

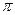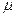Тогда, по теореме о циркуляции, В 2 r = _oN I, откуда следует, что
магнитная индукция внутри тороида (в вакууме)

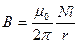(3.10.1)

где N - число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и В2 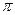r= 0. Эго означает, что поле вне тороида отсутствует (что показывает и опыт).