Циркуляция вектора В для магнитного поля в вакууме.

Аналогично циркуляции вектора напряженности электростатического поля введем циркуляцию вектора магнитной индукции. Цирку­ляцией вектора В по заданному замкнутому контуру называется интеграл

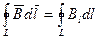
где d 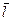- вектор элементарной длины контура, направленной вдоль обхода кон­тура. В_l=В cosa - составляющая вектора 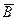в направлении касательной к конту­ру, a - угол между векторами 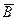и d .

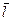Закон полного тока для магнитного поля в вакууме (теорема о циркуляции
вектора 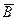) читается так: циркуляция вектора 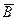по произвольному замкнутому
контуру равна произведению магнитной постоянной 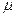₀ на алгебраическую
сумму токов, захватываемых этим контуром:

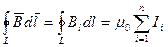(3.9.1)

где n - число проводников с током, охватываемых контуром L произвольной формы. Каждый ток учитывается столько раз, сколько раз он охватывается кон­туром. Положительным считается ток, направление которого связано с направ­лением обхода по контуру правилом правого винта, ток противоположного на правления считается отрицательным. Например, для системы токов, изображенных на рис. 3.9.1,

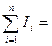I₁+2*I₂-0*I₃-I₄

Выражение (3.9.1) справедливо только для поля в вакууме^ 1*оскольку для пиля в веществе необходимо учитывать молекулярные токи.

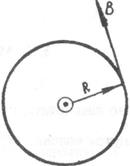
Продемонстрируем справедливость теоремы о циркуляции вектора 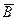на примере магнитного поля прямого тока I, перпендикулярного плоскости черте­жа и направленного к нам (рис.3.9.2).

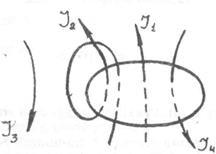
Рис.3.9.1 Рис.3.9.2

Представим себе замкнутый контур в виде окружности радиуса R. В каж­дой точке этого контура вектор 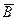одинаков по модулю и направлен по каса­тельной к окружности. Следовательно, циркуляция вектор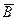а равна

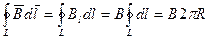
Согласно выражению (3.9.1), получим В2 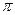R = 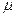₀1, откуда

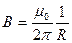
Таким образом, исходя из теоремы о циркуляции вектора 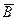, получили вы­ражение для магнитной индукции поля прямого тока, выведенное выше.

Сравнивая выражения для циркуляции векторов 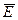и 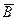, ви­дим, что между ними существует принципиальное различие. Циркуляция век­тора 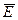электростатического поля всегда равна нулю, т.е. электростатическое поле является потенциальным. Циркуляция вектора 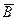магнитного поля не равна нулю. Такое поле называется вихревым.

Теорема о циркуляции вектора 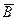имеет в учении о магнитном поле такое же значение, как теорема Гаусса в электростатике, т.к. позволяет находить маг­нитную индукцию поля без применения закона Био-Савара-Лапласа.