Работа по перемещению проводника и контура стоком в магнитном поле.

На проводник с током в магнитном поле действуют силы, определяемые законом Ампера. Если проводник не закреплен (рис.38), то под действием силы Ампера он будет в магнитном поле перемещаться, магнитное поле совершает работу по перемещению проводника с током. Для определения этой работы рас­смотрим проводник длиной t с током I (он может свободно перемещаться), помещенный в однородное внешнее магнитное поле, перпендикулярное плоскости контура. При указанных на рис. 3.12.1 направлениях тока и поля сила, направ­ление которой определяется по правилу левой руки, а значение - по закону Ампера, равна F=IВl.

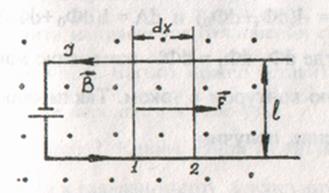Под действием силы проводник перемес­тится параллельно самому себе на отрезок dx из положения 1 в положение 2. Работа, совершаемая магнитным полем, равна

dA=Fdx=IBdS=IdФ,

­ Рис.3.12.1

т.к. ldx = dS - площадь, пересекаемая проводником при его перемещении в магнитном поле, В dS = dФ - поток вектора магнитной индукции, пронизываю­щий эту площадь. Таким образом,

dA= IdФ, (3.12.1)

т.е. работа по перемещению проводника с током в магнитном поле равна про­изведению силы тока на магнитный поток, пересеченный движущимся провод­ником. Полученная формула справедлива и для произвольного направления вектора .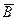

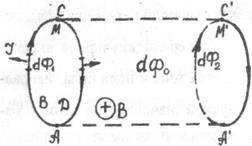
Вычислим работу по перемещению замкнутого контура с постоянным то­ком I в магнитном поле. Предположим, что контур М перемещается в плоско­сти чертежа и в результате бесконечно малого перемещения займет положение М', изображенное на рис. 3.12.2 штриховой линией. Направление тока в контуре (по часовой стрелке) и магнитного поля (перпендикулярно плоскости чертежа -за чертеж) указано на рисунке. Контур М мысленно разобьем на два соединен­ных своими концами проводника: ABC и CDA.

Работа dA, совершаемая силами Ампера при рассматриваемом перемещении контура в магнитном поле, равна алгеб­раической сумме работ по перемещению проводников ABC (dA₁) и CDA (dA₂),

dA=dA₁+dA₂

где dA₁=-I(dФ₁+dФ₀) и dA=-I(dФ₂+dФ₀)

Рис.3.12.2

Подставляя, получим dA = I (dФ2-dФ2), где dФ2-dФl = dФ' - изменение магнитного потока через площадь, ограниченную контуром с током. Таким обра­зом, dA = I dФ'. Проинтегрировав это выражение, получим

А = 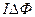, (3.12.2)

т.е. работа по перемещению замкнутого контура с током в магнитном поле рав­на произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром Формула (3.12.2) остается в произвольном магнитном поле.