Закон Био-Савара-Лапласа. Магнитное поле прямолинейного и кругового токов.

Закон Био-Савара-Лапласа позволяет вычислить магнитную индукцию поля, созданного элементом тока Id на расстоянии от него:

dB = , (14-5)

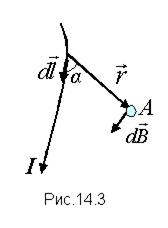
т.е. индукция магнитного поля, создаваемого элементом тока Id точке А, (рис.14.3), на расстоянии r от него, пропорциональна ве­личине элемента тока и синусу угла a, равного углу между направле­ниями элемента тока Id и , а также обратно пропорциональна квадрату расстояния между ними; 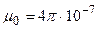Гн / м - магнитная посто­янная.

Закон Био - Савара - Лапласа в векторной форме имеет вид:

d = 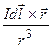. (14-6)

Закон Био - Савара - Лапласа позволяет вычислить магнитную индукцию поля любых систем токов, используя принцип суперпозиции магнитных поля

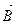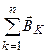= . (14-7)

Применим закон Био - Савара - Лапласа и принцип суперпозиции (14-7) к расчету магнитных полей следующих токов:

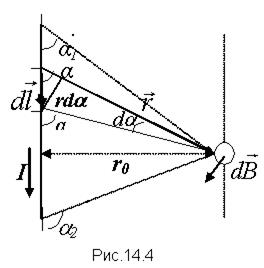
1) Магнитное поле прямолинейного тока.

Из рис.14.4 с учетом (14-6) находим, что d 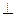плоскости, в которой лежат d и 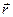; далее можно найти 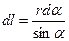,откуда, принимая во внимание, что 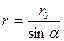получаем 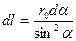. С учетом этого из (14-5) находим:

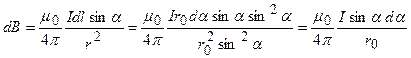
интегрируя последнее равенство, получаем

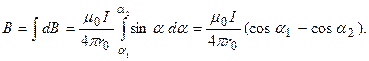(14-8)

Для бесконечно длинного проводника , 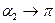и из (8) следует, что

(14-9)

2) Магнитное поле кругового тока.Можно показать, что магнитная индукция поля, создан­ного круговым током радиуса R, на расстоянии r₀ вдоль перпендикуляра, восстановленного из центра контура, (рис.14.5), будет

(14-10)

В частности, в центре кругового тока ,

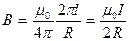. (14-11)

Для плоской катушки, состоящей из N, витков магнитная индукция на оси катушки

. (14-12)

При больших расстояниях от контура, т. е. при r₀ >> R из (14-10) получим

(14-13)