Закон Ампера. Взаимодействие параллельных токов.

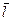Магнитное поле оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током, Ампер установил, что сила d ,с которой магнитное поле действует на элемент проводника d с током, находящийся в магнитном поле, прямо пропорциональна силе тока I в проводнике и векторному произведению элемента длиной d 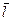проводника на магнитную индукцию :

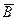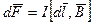(3.3.1)

Направление вектора d может быть найдено, согласно (3.3.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 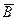, а четыре вы­тянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера вычисляется по формуле

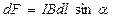(3.3.2)

где a -угол между векторами d 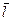и .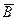

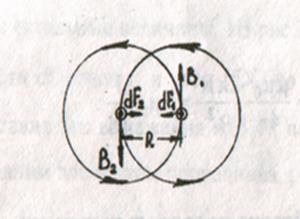Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I₁ и I₂ (направления токов указаны на рис. 3.3.2), расстояние между которыми равно R.

Каждый из проводников создает магнит­ное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I₁ на элемент dl второго проводника с током 1₂.

Ток I₁ создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора 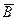задается правилом правого винта, его модуль по формуле (3.3.2) равен

Рис.3.3.1

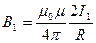
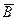Направление силы d ₁ , с которой поле ₁ действует на участок dl, второ­го тока, определяется по правилу левой руки и указано на рис 3.3.1. Модуль силы,
согласно (3.3.2), с учетом того, что угол, а между элементами тока 1₂ и вектором
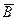₁ прямой равен

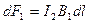
или, подставляя значения для В₁ , получим

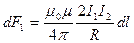(3.3.3)

Рассуждая аналогично, можно показать, что сила dF₂, с которой магнитное поле тока I₂ действует на элемент dl первого проводника с током I₁, направле­на в противоположную сторону и по модулю равна

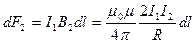(3.3.4)

Сравнение выражений (3.10) и (3.11) показывает, что

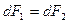
т.е. два параллельных тока одинакового направления притягиваются друг к другу с силой

(3.3.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания.