Мандатная постоянная. Единицы магнитной индукции напряженности магнитного поля.

Если два параллельных проводника с током находятся в вакууме ( 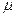=1), то сила взаимодействия на единицу длины проводника равна

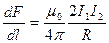(3.4.1)

Для нахождения числового значения 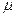₀ воспользуемся определением ампера, согласно которому при I₁=I₂=1А и R=1м,

Подставив это значение в формулу (3.4.1), получим 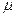₀= 4 -10^-7 Н/А² = 4 -10^-7 Гн/м, где генри (Гн) - единица индуктивности.

Закон Ампера позволяет определить единицу магнитной индукции В. Предположим, что элемент проводника dl с током I перпендикулярен направ­лению магнитного поля. Тогда закон Ампера запишется в виде dF = IBdl, откуда

Единица магнитной индукции - тесла (Тл): 1Гл - магнитная индукция тако­го однородного магнитного поля, которое действует с силой в 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток в 1 А:

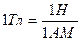
Так как 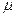₀= 4 -10^-7 Н/А² , а в случае вакуума ( 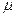=1), В= 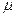₀Н, то для данного случая

Единица напряженности магнитного поля – ампер на метр (А/м): 1 А/м – напряженность такого поля, магнитная индукция которого в вакууме равна 4 -10^-7 Тл.

3.5 Магнитное поле движущегося заряда.

Каждый проводник с током создает в окружающем пространстве магнит­ное поле. Электрический же ток представляет собой упорядоченное движение электрических зарядов. Поэтому можно сказать, что любой движущийся в вакууме или в среде заряд создает вокруг себя магнитное поле. В результате обобщения опытных данных был установлен закон, определяющий поле В то­чечного заряда Q, свободно движущегося со скоростью v. Под свободным дви­жением заряда понимается его движение с постоянной скоростью. Этот закон выражается формулой

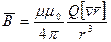(3.5.1)

где r - радиус-вектор, проведенный от заряда Q к точке наблюдения М (рис.3.5.1).

Вектор 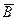направлен перпендикулярно плоскости, в которой расположены векторы 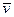и 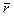, а именно: его направление совпадает с на­правлением поступательного движения правого винта при его вращении от 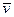к .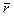

Рис. 3.5.1

Модуль магнитной индукции вычисляется по формуле

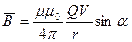(3.5.2)

где а - угол между векторам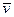и и .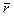

Движущийся заряд со своими магнитным свойствам эквивалентен элементу тока:

Id 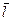=Q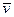

Приведенные закономерности (3.5.1) и (3.5.2) справедливы лишь при малых скоростях (v«c) движущихся зарядов, когда электрическое поле свободно движущегося заряда можно считать электростатическим, т.е. создаваемым не­подвижным зарядом, находящимся в той точке, где в данный момент времени находится движущийся заряд.

Формула (3.5.1) определяет магнитную индукцию положительного заряда, движущегося со скоростью v. Если движется отрицательный заряд, то Q надо заменить на -Q. Скорость v - относительная скорость, т.е. скорость относительно наблюдателя. Вектор 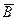в рассматриваемой системе отсчета зависит как от времени, так и от положения точки М наблюдателя. Поэтому следует подчерк­нуть относительный характер магнитного поля движущегося заряда. Магнитное поле свободно движущихся зарядов было измерено академиком А.Ф.Иоффе.