Преобразование Лапласа

При управлении объектами важно уметь вычислять выходной сигнал системы при известном входном. Для решения такой задачи необходимо решать ДУ. Чтоб упростить процедуру, существует специальное преобразование, которое позволяет заменить решение ДУ алгебраическими вычислениями.

Для функции 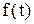вводится преобразование Лапласа, которое обозначается как .

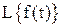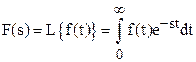(7.15)

Функция F(s) называется изображением для функции f(t) (оригинала). Здесь s – это комплексная переменная, которая выбирается так, чтобы интеграл (7.15) сходился.

Обратное преобразование Лапласа 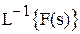позволяет вычислить оригинал f(t) по известному изображению F(s).

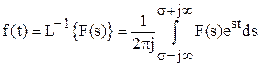(7.16)

Где 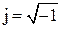, а постоянная 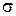выбирается так, чтобы интеграл сходился.

На практике вместо интеграла чаще всего используют готовые таблицы, по которым можно сразу определить изображение по оригиналу и наоборот.

Например, изображение Лапласа для единичного ступенчатого сигнала

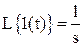
А изображение Лапласа для экспоненциального сигнала 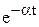имеет вид:

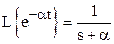
Свойства преобразования Лапласа:

1. Выполнение принципа суперпозиции как для прямого так и для обратного преобразования Лапласа:

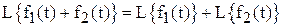
2. Изображение для производной функции равно:

,

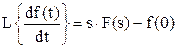где F(s) – изображение функции f(t), и f(0) – ее значение при t=0.

Поэтому при нулевых начальных условиях изображение производной равно изображению функции умноженному на s. А для построения изображения i-той производной нужно умножить изображение функции на .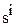

Иногда используют передаточную функцию как отношение изображений по Лапласу входного и выходного сигналов звена и обозначают: .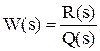

Здесь важно, что переход от одного вида передаточной функции к другому осуществляется формальной заменой pна sпри нулевых начальных условиях.