Линеаризация моделей

Внимание! При дальнейшем изложении материала будет использоваться такое понятие, как динамическое звено. Звено, представляет собой удобное математическое образование (виртуальное), которое описывается дифференциальным уравнением и представляется в виде прямоугольника со входами и выходами (вспомните, структурную схему объекта). Уравнение звена выражает зависимость между входными и выходными величинами данного звена. Динамическое уравнение звена (математическая модель звена) составляется по правилам соответствующей технической науки (звено может представлять собой тепловой двигатель, электрическую машину, механическую передачу, электрическую цепь и т.д.).

Вспомним, что принципиальным требованием к моделям объектов является отражение динамики во взаимосвязи между входными и выходными переменными. Поэтому входные и выходные переменные рассматриваются как процессы (их мы уже научились моделировать на компьютере). А модели преобразования воздействий, т.е. связь между входными и выходными переменными, математически должны описываться дифференциальными уравнениями.

Модель должна отражать существенные для исследователя свойства объекта. С одной стороны, модель должна как можно лучше отражать свойства реального объекта или системы, т.е. быть достаточно сложной. С другой стороны, она должна быть достаточно простой, чтоб ее составление занимало приемлемое время. Поэтому обычно стремятся к упрощениям при получении моделей.

Все модели реальных систем – нелинейные, так как всегда существует предельно допустимое значение входного сигнала и при его превышении объект может просто выйти из строя или даже разрушиться. Методы исследования нелинейных систем очень сложны математически.

Поэтому главным упрощением, к которому стремятся, является линеаризация моделей – использование для описания свойств объектов линейных дифференциальных уравнений.

Линеаризация допустима в следующих случаях:

1) аргумент линеаризуемой функции и сама функция изменяются на ограниченных интервалах;

2) нелинейная функция является гладкой (без разрывов) и монотонной (возрастающая или убывающая).

Идея линеаризации заключается в том, что в системах регулирования (поддержания заданных значений) сигналы мало отклоняются от рабочей точки – некоторого положения равновесия, в котором все сигналы имеют нужные значения и их производные равны нулю.

В общем случае процесс линеаризации связан с разложением нелинейной функции в ряд Тейлора в окрестности некоторой внутренней точки интервала изменения переменной и последующим отбрасыванием всех членов ряда со степенью превышающей единицу.

Рассмотрим линеаризацию на простом примере. Пусть дано звено, у которого взаимосвязь в статически установившихся режимах между входной (х) и выходной (у) переменными нелинейна, т.е. имеющее нелинейную статическую характеристику q(x). Используя понятие математической модели типа «вход-выход», изобразим его структурную схему (рис. 7.1):

Рис. 7.1

Пусть также входная (аргумент) и выходная (функция) переменные этого звена изменяются в некоторой окрестности точки С (х₀, у₀), заданной интервалами х Î [x₁, x₂], y Î [y₁, y₂], см. рис. 7.2.

Рис. 7.2

Раскладывая исходную нелинейную зависимость q(x) в окрестности точки C(x₀, y₀) в ряд Тейлора, и отбрасывая нелинейные члены, получим следующую зависимость (7.1):

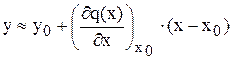, (7.1)

которая представляет собой аналитическое выражение линеаризованной статической характеристики звена по каналу «х – у», т.е. статической характеристики линейной модели звена по этому каналу.

Значение частной производной при значении х = х₀, k = 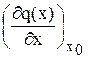называется коэффициентом передачи звена.

Графическая интерпретация процедуры линеаризации: В точке С(х₀, у₀) проводим касательную к кривой у = q(x) (ее угловой коэффициент tg(a) = k). На отрезке [х₁, х₂] кривая у = q(x) заменяется прямой y = y₀ + k(x – x₀), которая и представляет собой линеаризованную статическую характеристику звена.

Преобразуем выражение для статической характеристики звена от формы, когда мы оперируем с абсолютными значениями переменных, к форме, когда переменные задаются в приращениях относительно координат точки С. Для этого преобразуем выражение (7.1) к виду: у – у₀ = k(x – x₀). Обозначим: у – у₀ = Dу, а х – х₀ = Dх. Получаем линеаризованное уравнение звена в приращениях (отклонениях) от точки С: Dу = kDх.

Замечание: линеаризованная характеристика может быть корректно использована только на интервале линеаризации (изменение аргумента на отрезке от х₁ до х₂).

Примеры функций, для которых рассмотренная процедура линеаризации характеристик недопустима, см. рис. 7.3 и 7.4:

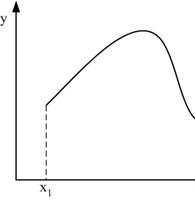
Рис. 7.3 Рис. 7.4