Передаточная функция. Дифференциальное уравнение звена (системы) в общем виде можно представить в виде:
Дифференциальное уравнение звена (системы) в общем виде можно представить в виде:
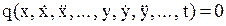 . (7.2)
. (7.2)
После перевода уравнения (7.2) к переменным в отклонениях и его линеаризации, уравнение принимает вид (8.3):
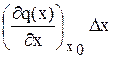 +
+ 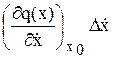 +
+ 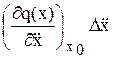 + … +
+ … + 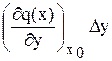 +
+
+ 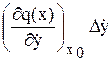 +
+ 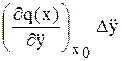 + … = 0, (7.3)
+ … = 0, (7.3)
где 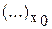 обозначает, что для частной производной вычислено ее значение в точке С(х0, у0).
обозначает, что для частной производной вычислено ее значение в точке С(х0, у0).
Возвращаясь к структурной схеме модели звена типа «вход – выход», изменим ее с учетом появившихся обозначений:

В теории систем автоматического управления приняты определенные формы записи дифференциальных уравнений, придающие их коэффициентам определенный физический смысл. Рассмотрим это на примере уравнения (7.3), считая его второго порядка. Осуществим следующие действия:
1) выходную переменную Dу оставим в левой части, а входную переменную Dх перенесем в правую часть уравнения:
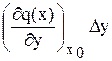 +
+ 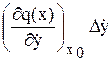 +
+ 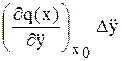 =
=
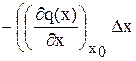 +
+ 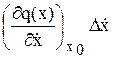 +
+ 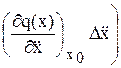 ; (7.4)
; (7.4)
2) разделим обе части уравнения на коэффициент перед приращением выходной величины Dу:
Dу + 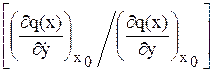
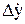 +
+ 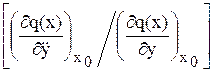
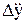 =
=
= 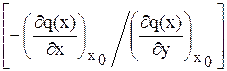 Dх +
Dх + 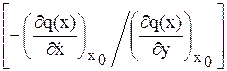
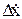 +
+
+ 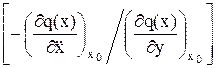
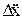 ; (7.5)
; (7.5)
3) обозначим полученные коэффициенты перед переменными символами, отражающими их физический смысл и размерность:
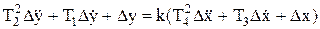 . (7.6)
. (7.6)
Для лучшего понимания рассмотрим, как были получены коэффициенты k и Т2, их размерность и общепринятые названия:
|
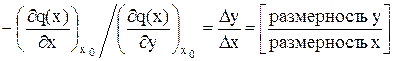 – ; (7.7)
– ; (7.7)
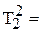
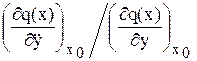 =
= 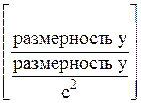 = [c2] (7.8)
= [c2] (7.8)
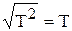 – постоянная времени. (7.9)
– постоянная времени. (7.9)
Перепишем (7.6) в развернутом виде:
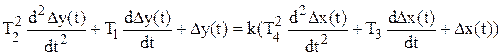 . (7.10)
. (7.10)
Введем оператор дифференцирования 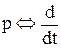 , который действует на сигнал
, который действует на сигнал 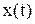 по правилу
по правилу 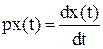 . Здесь важно, что запись
. Здесь важно, что запись 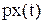 обозначает не умножение оператора
обозначает не умножение оператора 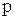 на сигнал, а действие этого оператора, то есть дифференцирование
на сигнал, а действие этого оператора, то есть дифференцирование 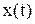 .
.
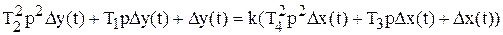 (7.11)
(7.11)
или 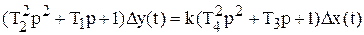 . (7.12)
. (7.12)
Используемые в данном уравнении коэффициенты приводят все слагаемые уравнения к одной размерности – размерности выходной переменной.
Замечание: в дальнейшем будем рассматривать дифференциальные уравнения только в отклонениях. Поэтому, для сокращения записи символ «D» использовать не будем.
С учетом данного замечания перепишем уравнение (7.12):
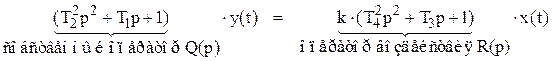 , (7.13)
, (7.13)
В компактной форме: Q(p)y(t) = R(p)x(t), y(t) = 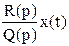 . (7.14)
. (7.14)
Полученное выражение является символической записью уравнения (7.4), которой удобно пользоваться. И запись (7.14) означает не умножение, а действие сложного оператора на сигнал 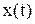 .
.
Функция 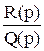 обозначается
обозначается 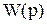 и называется передаточной функцией. Она полностью описывает связи между входом и выходом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
и называется передаточной функцией. Она полностью описывает связи между входом и выходом объекта при нулевых начальных условиях, но не учитывает его внутреннее устройство.
Дата добавления: 2015-05-30; просмотров: 1008;
