Проверка гипотезы о значении математического ожидания
Пусть из генеральной совокупности 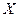 , распределенной по нормальному закону с параметрами
, распределенной по нормальному закону с параметрами 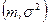 при неизвестном математическом ожидании
при неизвестном математическом ожидании 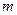 и неизвестной дисперсии
и неизвестной дисперсии 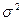 , взята случайная выборка
, взята случайная выборка 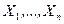 объемом
объемом 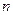 и вычислена выборочная средняя арифметическая
и вычислена выборочная средняя арифметическая
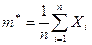 ,
,
а 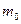 и
и 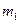 — определенные значения параметра
— определенные значения параметра 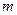 . Для проверки нулевой гипотезы
. Для проверки нулевой гипотезы 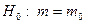 при конкурирующей гипотезе
при конкурирующей гипотезе 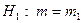 используют статистику
используют статистику
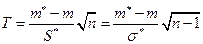 , (9.2.1)
, (9.2.1)
которая при выполнении нулевой гипотезы 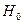 имеет
имеет 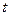 ‑ распределение (распределение Стьюдента) с
‑ распределение (распределение Стьюдента) с 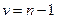 степени свободы.
степени свободы.
Учитывая соотношения (9.1.1) — (9.1.3), определяем границы 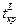 и
и 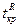 критической области по таблицам
критической области по таблицам 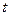 ‑ распределения (распределения Стьюдента) или используя функцию СТЬЮДРАСПОБР(вероятность; степени_свободы) из EXCEL, или используя функцию qt(p, d) из MATHCAD.
‑ распределения (распределения Стьюдента) или используя функцию СТЬЮДРАСПОБР(вероятность; степени_свободы) из EXCEL, или используя функцию qt(p, d) из MATHCAD.
При проверке нулевой гипотезы 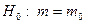 при известной дисперсии
при известной дисперсии 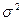 используют статистику
используют статистику
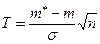 , (9.2.2)
, (9.2.2)
которая при выполнении нулевой гипотезы 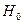 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 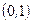 .
.
Учитывая соотношения (9.1.1) — (9.1.3), определяем границы 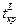 и
и 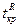 критической области по таблицам нормального распределения с параметрами
критической области по таблицам нормального распределения с параметрами 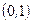 или используя функцию НОРМСТОБР(вероятность) из EXCEL, или используя функцию qnorm(ν, m, σ) из MATHCAD.
или используя функцию НОРМСТОБР(вероятность) из EXCEL, или используя функцию qnorm(ν, m, σ) из MATHCAD.
Пример 1. Поставщик двигателей утверждает, что средний срок их службы равен 800 ч. Для выборки из 17 двигателей средний срок службы оказался равным 865 ч. При «исправленном» среднем квадратичном отклонении 120 ч. Проверить гипотезу о том, что значение 800 является математическим ожиданием при 1% уровне значимости.
m Решение. Предположим, что случайная величина среднего времени службы подчинена нормальному закону о числовом значении математического ожидания нормально распределённой величины (генеральной средней) при неизвестной генеральной дисперсии. В этом случае в качестве критерия выбирают функцию
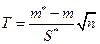 ,
,
где 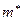 — выборочная средняя,
— выборочная средняя, 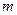 — математическое ожидание,
— математическое ожидание, 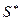 — «исправленное» выборочное среднее квадратичное отклонение. Случайная величина
— «исправленное» выборочное среднее квадратичное отклонение. Случайная величина 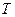 имеет
имеет 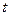 ‑ распределение (распределение Стьюдента) с
‑ распределение (распределение Стьюдента) с 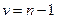 степени свободы.
степени свободы.
Требуется найти критическую область для нулевой гипотезы 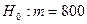 при альтернативной гипотезе
при альтернативной гипотезе 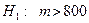 .
.
Критическая область правосторонняя, 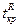 находим из условия
находим из условия 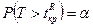 .
.
При 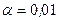 и
и 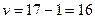 в таблице
в таблице 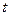 ‑ распределения находим
‑ распределения находим 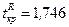 . Таким образом, критическая область
. Таким образом, критическая область 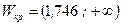 . Найдем расчетное значение
. Найдем расчетное значение 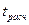 , полагая
, полагая 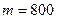 :
:
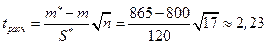 .
.
Очевидно, что найденное значение 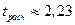 попадает в критическую область. Таким образом, нулевая гипотеза не подтверждается. l
попадает в критическую область. Таким образом, нулевая гипотеза не подтверждается. l
Дата добавления: 2015-05-28; просмотров: 4591;
