Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей
Пусть 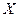 и
и 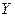 — две генеральные совокупности, распределенные по нормальному закону с неизвестными дисперсиями
— две генеральные совокупности, распределенные по нормальному закону с неизвестными дисперсиями 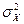 и
и 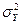 . Из генеральных совокупностей взяты две независимые выборки
. Из генеральных совокупностей взяты две независимые выборки 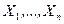 и
и 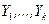 и вычислены исправленные выборочные дисперсии
и вычислены исправленные выборочные дисперсии 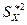 и
и 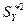 .
.
Требуется проверить нулевую гипотезу 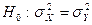 . В данном случае используется статистика
. В данном случае используется статистика
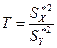 , (9.5.1)
, (9.5.1)
которая имеет F‑распределение (распределение Фишера) с 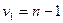 и
и 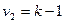 степенями свободы, если
степенями свободы, если 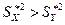 , и
, и
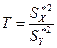 , (9.5.2)
, (9.5.2)
с числом степеней свободы 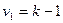 и
и 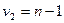 , если
, если 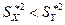 .
.
Если задаться уровнем значимости 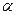 , то можно построить критические области для проверки нулевой гипотезы при двух альтернативных гипотезах:
, то можно построить критические области для проверки нулевой гипотезы при двух альтернативных гипотезах:
a) 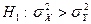 , если
, если 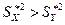 , или
, или 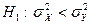 , если
, если 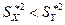 . В этом случае критическая область правостороння
. В этом случае критическая область правостороння 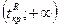 . Граница
. Граница 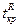 критической области определяется из условия
критической области определяется из условия 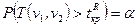 ;
;
b) 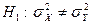 . В этом случае критическая область двусторонняя. Однако можно использовать только правостороннюю область
. В этом случае критическая область двусторонняя. Однако можно использовать только правостороннюю область 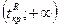 , где граница
, где граница 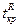 определяется из условия
определяется из условия 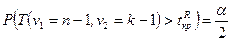 , если
, если 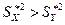 , и из условия
, и из условия 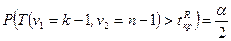 , если
, если 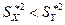 .
.
Пример 4.При измерении производительности двух агрегатов получены следующие результаты в кг вещества за час работы:
| № замера | |||||
| Агрегат A | 14,1 | 10,1 | 14,7 | 13,7 | 14,0 |
| Агрегат B | 14,5 | 13,7 | 12,7 | 14,1 |
При уровне значимости 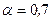 проверить гипотезу о равенстве дисперсий.
проверить гипотезу о равенстве дисперсий.
m Решение.Проверим нулевую гипотезу 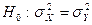 при альтернативной гипотезе
при альтернативной гипотезе 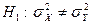 . Вычислим «исправленные» выборочные дисперсии
. Вычислим «исправленные» выборочные дисперсии 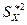 и
и 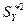 . Для этого сначала найдем выборочные средние
. Для этого сначала найдем выборочные средние 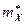 и
и 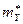 :
:
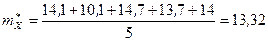 ;
; 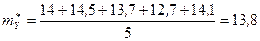 .
.
Тогда
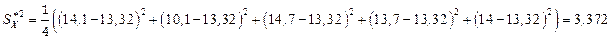 ;
;
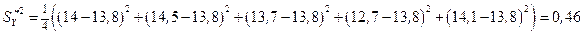 .
.
Учитывая, что 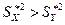 , определяет
, определяет 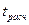 :
:
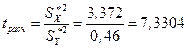 .
.
Критическое значение 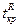 находим из условия
находим из условия
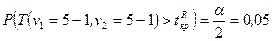
По таблице F‑распределения (распределения Фишера) с 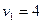 и
и 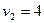 степенями свободы определяем
степенями свободы определяем 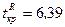 .
.
Так как число 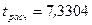 попадает в критическую область
попадает в критическую область 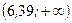 , то гипотезу о равенстве дисперсий отвергаем. l
, то гипотезу о равенстве дисперсий отвергаем. l
Замечание.Границу критической области было можно определить и не используя таблицы, например:
§ используя функцию FРАСПОБР(вероятность; степени_свободы1; степени_свободы2) из EXCEL. При этом задаваемый уровень значимости используется как аргумент «вероятность». В рассматриваемом примере получаем 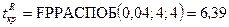 ;
;
§ используя функцию qF(P,d1,d2) из MATHCAD, где P — доверительная вероятность 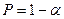 , d1 и d2 степени свободы. В рассматриваемом примере получаем
, d1 и d2 степени свободы. В рассматриваемом примере получаем 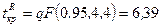 .
.
Дата добавления: 2015-05-28; просмотров: 1809;
