Глава 9. Проверка статистических гипотез
Основные понятия
Определение. Статистической гипотезой называется любое предположение 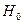 (гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения.
(гипотеза) о виде закона распределения генеральной совокупности или о числовых значениях параметров закона распределения.
Определение. Правило, по которому гипотеза 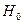 принимается или отвергается, называется статистическим критерием.
принимается или отвергается, называется статистическим критерием.
Проверяемую гипотезу 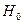 называют нулевой, а противоположную ей гипотезу
называют нулевой, а противоположную ей гипотезу 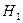 называют альтернативной.
называют альтернативной.
Схема проверки нулевой гипотезы:
1. Используя проверочные данные 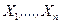 и учитывая условия задачи, принимают нулевую гипотезу
и учитывая условия задачи, принимают нулевую гипотезу 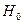 и альтернативную гипотезу
и альтернативную гипотезу 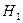 .
.
2. По случайной выборке 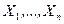 определяется функция
определяется функция 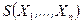 , называемая статистикой, для которой будет известен точный или приближённый закон распределения.
, называемая статистикой, для которой будет известен точный или приближённый закон распределения.
3. По заранее выбранной малой вероятности 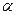 определяется критическая область
определяется критическая область 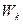 , для которой
, для которой 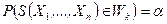 . И если величина
. И если величина 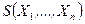 , вычисляется при конкретной выборке
, вычисляется при конкретной выборке 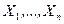 , окажется вне критической области
, окажется вне критической области 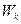 , то гипотеза
, то гипотеза 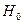 принимается, а если она окажется в области
принимается, а если она окажется в области 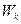 , то гипотеза
, то гипотеза 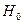 отвергается (или принимается гипотеза
отвергается (или принимается гипотеза 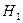 ). При этом возможны 4 случая, которые представлены в таблице 9.1
). При этом возможны 4 случая, которые представлены в таблице 9.1
Таблица 9.1
Принимается 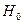
| Отвергается 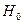
| |
Верна гипотеза 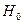
| Правильное решение | Ошибка первого рода |
| вероятность | 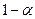
| 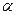
|
Верна 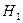
| Ошибка второго рода | Правильное решение |
| вероятность | 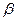
| 
|
Определение. Вероятность 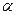 допустить ошибку первого рода называется уровнем значимости критерия.
допустить ошибку первого рода называется уровнем значимости критерия.
Определение. Вероятность 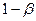 не допустить ошибку второго рода называется мощностью критерия.
не допустить ошибку второго рода называется мощностью критерия.
Если использовать терминологию качества продукции, то 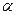 — это «риск поставщика», связанный с забраковкой по результату выборки всей партии товара, соответствующей стандарту, а
— это «риск поставщика», связанный с забраковкой по результату выборки всей партии товара, соответствующей стандарту, а 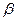 — «риск потребителя», связанный с принятием по результатам выборки партии товара, не соответствующей стандарту.
— «риск потребителя», связанный с принятием по результатам выборки партии товара, не соответствующей стандарту.
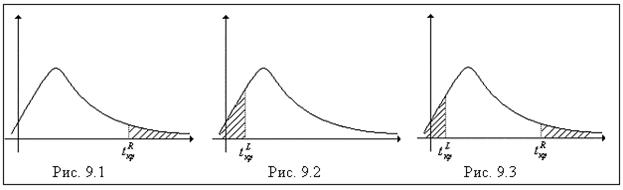
Возможны три варианта расположения критической области:
1. Правосторонняя критическая область (рис 9.1), состоящая из интервала 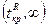 , где
, где 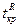 определяется из условия:
определяется из условия:
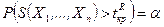 . (9.1.1)
. (9.1.1)
2. Левосторонняя критическая область (рис 9.2), состоящая из интервала 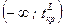 , где
, где 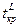 определяется из условия:
определяется из условия:
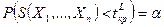 . (9.1.2)
. (9.1.2)
3. Двусторонняя критическая область (рис 9.3), состоящая из интервалов 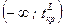 и
и 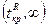 , где точки
, где точки 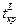 и
и 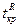 определяется из условий:
определяется из условий:
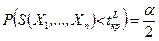 и
и 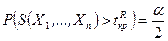 . (9.1.3)
. (9.1.3)
В следующих параграфах рассмотрим несколько конкретных практических примеров.
Дата добавления: 2015-05-28; просмотров: 1380;
