Проверка гипотезы о распределении. Критерий Пирсона

Пусть 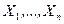— выборка, произведенная из генеральной совокупности 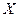, с неизвестной функцией распределения 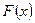. Проверяется нулевая гипотеза 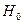, утверждающая, что генеральная совокупность распределена по закону, имеющему функцию распределения 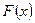, равную функции 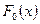, т.е. проверяется нулевая гипотеза 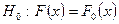. При этом альтернативной гипотезой является .

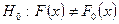Наибольшее применение при проверке согласования закона распределения, т.е. проверке нулевой гипотезы 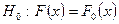, является критерий Пирсона или критерий 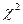(хи-квадрат).

Наблюдаемое значение критерия (статистика) вычисляется по следующей формуле:

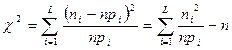. (9.6.1)

Согласно теореме К. Пирсона, при 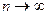статистика (9.6.1) имеет 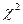‑распределение с 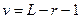степенями свободы, где 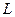— число групп (интервалов) выборки, 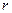— число параметров предполагаемого распределения.