Метод максимального правдоподобия. Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок

Метод максимального правдоподобия является наиболее распространенным методом нахождения оценок. Метод максимального правдоподобия опирается на использование условий экстремума функций одной или нескольких случайных величин. В качестве такой функции используется функция правдоподобия.

Определение. Функцией правдоподобияназывается функция

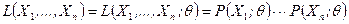(8.3.1)

в дискретном случае и

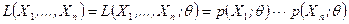(8.3.2)

в непрерывном случае.

В функции правдоподобия 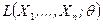элементы выборки 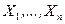являются фиксированными параметрами, а 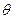— аргументом.

Определение. Оценкой максимального правдоподобияназывается такое 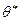, для которого

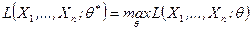. (8.3.3)

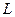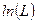Поскольку и принимают максимум при одном и том же значении аргумента 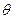, то при практической реализации метода максимального правдоподобия удобно использовать не саму функцию правдоподобия, а ее логарифм.

Определение. Уравнением правдоподобияназывается уравнение

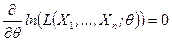. (8.3.4)

В случае, когда теоретическая функция распределения 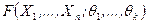зависит от нескольких параметров 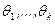, при применении метода максимального правдоподобия вместо уравнения (8.3.4) необходимо использовать систему уравнений

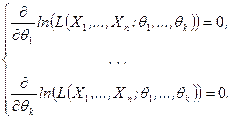(8.3.5)

Пример 4. Найти оценки параметров 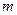(математическое ожидание) и 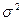(дисперсия) нормального закона распределения.

m Решение. Нормальный закон распределения характеризуется плотностью распределения

.

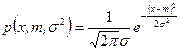Функция правдоподобия примет вид:

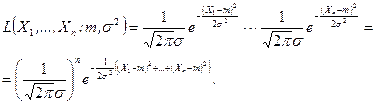(8.3.6)

Логарифмируя выражение (8.3.6), получим

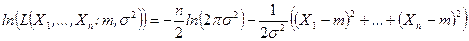. (8.3.7)

Подставляя (8.3.7) в систему (8.3.5), получим

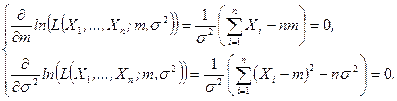(8.3.8)

Из первого уравнения системы (8.3.8) получаем

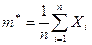, (8.3.9)

а из второго уравнения системы (8.3.8), с учетом (8.3.9), получаем

.

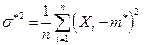Следует отметить, что полученная оценка является смещенной.

Читателю предлагается самостоятельно показать, что 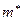и 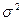доставляют максимум функции правдоподобия 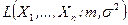. l